
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明:
时,证明:![]() ;
;
(3)试比较![]() 与
与![]()
![]() ,并证明你的结论。
,并证明你的结论。
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)求得![]() ,对
,对![]() 的范围分类讨论即可求得
的范围分类讨论即可求得![]() 的单调性。
的单调性。
(2)将![]() 转化成
转化成![]() ,证明
,证明![]() 恒成立,利用导数求得
恒成立,利用导数求得![]() ,问题得证。
,问题得证。
(3)由(2)可得:![]() ,整理得:
,整理得:![]() ,所以
,所以![]() ,整理
,整理![]() 得:
得:![]()
利用![]() 即可得:
即可得:![]() ,问题得解。
,问题得解。
(1)函数![]() 的定义域为:
的定义域为:![]() ,
,![]()
![]()
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
②当![]() 时,令
时,令![]() ,解得
,解得![]()
![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() , 所以
, 所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)当![]()
![]() 时,
时,![]() ,要证明
,要证明![]() ,
,
即证![]() ,即证:
,即证:![]() .
.
设![]() ,则
,则![]()
![]() ,令
,令![]() 得,
得,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以![]() 为极大值点,且
为极大值点,且![]() 在
在![]() 处取得最大值。
处取得最大值。
所以![]() ,即
,即![]() 。故
。故![]() .
.
(3)证明:![]() (当且仅当
(当且仅当![]() 时等号成立),即
时等号成立),即![]() ,
,
则有![]() +
+![]()
![]()
![]() ,
,
故:![]() +
+![]()


科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
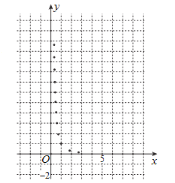
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关
关![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为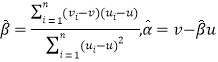 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品
,现安排甲组研发新产品![]() ,乙组研发新产品
,乙组研发新产品![]() .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品![]() 研发成功,预计企业可获得
研发成功,预计企业可获得![]() 万元,若新产品
万元,若新产品![]() 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润![]() 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在一个周期内的图象如图所示,A为图象的最高点,B,C为
在一个周期内的图象如图所示,A为图象的最高点,B,C为![]() 的图象与x轴的交点,且
的图象与x轴的交点,且![]() 为等边三角形.将函数
为等边三角形.将函数![]() 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的![]() 倍后,再向右平移
倍后,再向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.
的图象.

(1)求函数![]() 的解析式;
的解析式;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com