
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
分析 在单位圆x2+y2=1内随机均匀产生一点(x,y),其面积为1,使得$\left\{{\begin{array}{l}{\sqrt{3}x-y≥0}\\{x+\sqrt{3}y≥0}\end{array}}\right.$成立,其区域为单位圆的$\frac{1}{4}$,即可得出结论.
解答 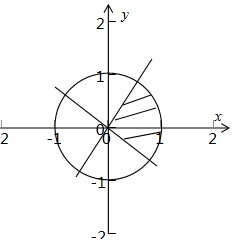 解:在单位圆x2+y2=1内随机均匀产生一点(x,y),其面积为1,
解:在单位圆x2+y2=1内随机均匀产生一点(x,y),其面积为1,
使得$\left\{{\begin{array}{l}{\sqrt{3}x-y≥0}\\{x+\sqrt{3}y≥0}\end{array}}\right.$成立,其区域为单位圆的$\frac{1}{4}$,其面积为$\frac{1}{4}$,
∴所求概率为$\frac{1}{4}$.
故选A.
点评 本题考查的知识点是几何概型,二元一次不等式(组)与平面区域,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=N(A)÷N求解.


科目:高中数学 来源: 题型:解答题
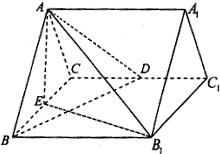 如图,已知正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,E为BC的中点.
如图,已知正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD=1,EC⊥BD,∠BCD=120°,EA=2,M是EC上的点,且EM=3MC.
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD=1,EC⊥BD,∠BCD=120°,EA=2,M是EC上的点,且EM=3MC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
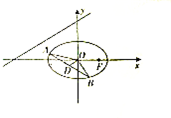 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F到直线x=$\frac{a^2}{c}$的距离为1.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F到直线x=$\frac{a^2}{c}$的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | $[0,2)∪\{-\frac{18}{e^2}\}$ | C. | $(0,2)∪\{-\frac{18}{e^2}\}$ | D. | $[0,2\sqrt{e})∪\{-\frac{18}{e^2}\}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com