
分析 将已知的二项式转化为:(1+x+$\frac{1}{{x}^{2}}$)10=(1+x+$\frac{1}{{x}^{2}}$)(1+x+$\frac{1}{{x}^{2}}$)…(1+x+$\frac{1}{{x}^{2}}$)(10个括号相乘),利用组合数的性质,即可求得其展开式中的常数项
解答 解:求${({1+x+\frac{1}{x^2}})^{10}}$═(1+x+$\frac{1}{{x}^{2}}$)(1+x+$\frac{1}{{x}^{2}}$)•…•(1+x+$\frac{1}{{x}^{2}}$)(10个括号相乘),
∴每个括号中都提供常数项1,有110种;
从10个括号中有选两个提供x项,从剩余的8个括号中选一个提供$\frac{1}{{x}^{2}}$,其余的括号中均提供1,有${C}_{10}^{2}$•${C}_{8}^{1}$ 种;
从10个括号中有选4个提供x项,从剩余的6个括号中选2个提供$\frac{1}{{x}^{2}}$,其余的括号中均提供1,有${C}_{10}^{4}$•${C}_{6}^{2}$ 种;
从10个括号中有选6个提供x项,从剩余的4个括号中选3个提供$\frac{1}{{x}^{2}}$,其余的括号中均提供1,有${C}_{10}^{6}$•${C}_{4}^{3}$种;
∴展开式中的常数项为1+${C}_{10}^{2}{•C}_{8}^{1}$+${C}_{10}^{4}{•C}_{6}^{2}$+${C}_{10}^{6}{•C}_{4}^{3}$=1+360+3150+840=4351.
点评 本题考查二项式系数的性质,熟练应用组合数的性质是解决问题的关键,突出考查转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
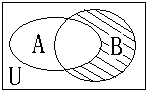
| A. | (∁UA)∩B | B. | (∁UA)∩(CUB) | C. | A∩(∁UB) | D. | A∪(∁UB) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额X(元) | [500,1000) | [1000,1500) | [1500,+∞) |
| 抽奖次数 | 1 | 2 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
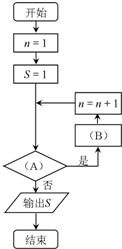 已知数列{an},a1=1,an+1=an+n,计算数列{an}的第20项.现已给出该问题算法的程序框图(如图所示).为使之能完成上述的算法功能,则在如图判断框中(A)处和(B)处依次应填上合适的语句是( )
已知数列{an},a1=1,an+1=an+n,计算数列{an}的第20项.现已给出该问题算法的程序框图(如图所示).为使之能完成上述的算法功能,则在如图判断框中(A)处和(B)处依次应填上合适的语句是( )| A. | n≤20,S=S-n | B. | n≤20,S=S+n | C. | n≤19,S=S-n | D. | n≤19,S=S+n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com