
若双曲线 -
-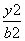 =1(a>0,b>0)的左、右焦点分别为F1和F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3两段,则此双曲线的离心率为________.
=1(a>0,b>0)的左、右焦点分别为F1和F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3两段,则此双曲线的离心率为________.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
已知双曲线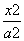 -
-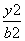 =1(a>0,b>0)的一个焦点与圆x2+y2-10x=0的圆心重合,且双曲线的离心率等于
=1(a>0,b>0)的一个焦点与圆x2+y2-10x=0的圆心重合,且双曲线的离心率等于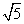 ,则该双曲线的标准方程为( ).
,则该双曲线的标准方程为( ).
A. -
-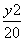 =1 B.
=1 B.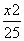 -
-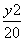 =1
=1
C.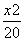 -
-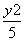 =1 D.
=1 D.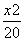 -
-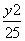 =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆C: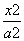 +
+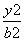 =1(a>b>0)的左、右焦点分别是F1,F2,离心率为
=1(a>b>0)的左、右焦点分别是F1,F2,离心率为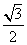 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,❶连接PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(3)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点.❷设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明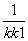 +
+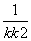 为定值,❸并求出这个定值.
为定值,❸并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两点M(-5,0)和N(5,0),若直线上存在点P,使|PM|-|PN|=6,则称该直线为“R型直线”.给出下列直线:①y=x+1;②y=2;③y=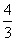 x;④y=2x+1,其中为“R型直线”的是( ).
x;④y=2x+1,其中为“R型直线”的是( ).
A.①② B.①③ C.①④ D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,已知椭圆C1: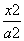 +
+ =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,点P(0,-1)是椭圆C1: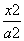 +
+ =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
(1)求椭圆C1的方程;
(2)求△ABD面积取最
大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题;
①设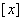 表示不超过
表示不超过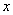 的最大整数,则
的最大整数,则
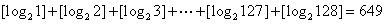 ;
;
②定义在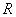 上的函数
上的函数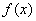 ,函数
,函数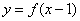 与
与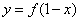 的图象关于
的图象关于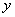 轴对称;
轴对称;
③函数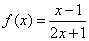 的对称中心为
的对称中心为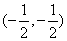 ;
;
④已知函数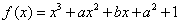 在
在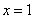 处有极值
处有极值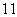 ,则
,则 或
或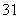 ;
;
⑤定义:若任意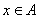 ,总有
,总有 ,就称集合
,就称集合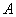 为
为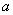 的“闭集”,已知
的“闭集”,已知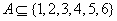 且
且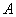 为
为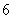 的“闭集”,则这样的集合
的“闭集”,则这样的集合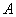 共有7个。
共有7个。
其中正确的命题序号是____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com