
如图所示,在梯形ABCD中,AB=10,CD=6,AD=BC=4,动点P从B点开始沿着折线BC、CD、DA前进至A,若P点运动的路程为x,△PAB的面积为y.

(1)写出y=f(x)的解析式,并求出函数的定义域;
(2)画出函数的图象并求出函数的值域.
|
思路分析:首先通过画草图可以发现,P点运动到不同的位置,y的求法是不同的(如图的阴影部分所示).
可以看出上述三个阴影三角形的底是相同的,它们的面积由其高来定,所以只要由运动里程x来求出各段的高即可. 解:(1)分类讨论: ①当P在BC上运动时,易知∠B=60°,则知 y= ②当P点在CD上运动时, y= ③当P在DA上运动时, y= 综上所述,函数的关系式为 y=f(x)= (2)f(x)的图象如图所示.
由图象可知y的取值范围是0≤y≤10 |
|
本题考查的是分段函数,这是一个实际问题,解题时要用到分类讨论思想及数形结合思想,这是多年的高考热点,也是今后高考命题的方向. (1)画出草图帮助分析时,要明确哪些是关键量,以及这些量的特点(变与不变); (2)对分段函数要选准线段的各端点. (3)可以通过画图判断函数的值域,这也是一种数形结合的解题思想. |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:全优设计必修五数学苏教版 苏教版 题型:044
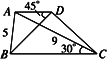
如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.求BD的长度.
查看答案和解析>>
科目:高中数学 来源:选修设计数学A4-1人教版 人教版 题型:047
如图所示,在梯形ABCD中,AD∥BC,∠C=90°,且AD+BC=AB,AB为⊙O的直径.
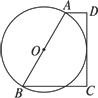
求证:⊙O与CD相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
![]()
(1)写出y=f(x)的解析式,指出函数的定义域;
(2)画出函数的图像并求出函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:

(2)如下图所示,设O是正六边形ABCDEF的中心.在图里的向量中

①写出与![]() 相等的向量;
相等的向量;
②写出与![]() 相等的向量;
相等的向量;
③写出与![]() 共线的向量;
共线的向量;
④写出与![]() 长度相等但方向相反的向量.
长度相等但方向相反的向量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com