练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，在梯形ABCD中，AD∥BC，∠C＝90°，且AD＋BC＝AB，AB为⊙O的直径．

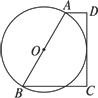
    求证：⊙O与CD相切．

    答案：
    解析：

    　　证明：过O作OE⊥CD，垂足为E．

    　　因为AD∥BC，∠C＝90°，

    　　所以AD∥OE∥BC．

    　　因为O为AB的中点，

    　　所以E为CD的中点．

    　　所以OE＝(AD＋BC)．

    　　又因为AD＋BC＝AB，

    　　所以OE＝AB，且等于⊙O的半径．

    　　所以⊙O与CD相切．

    　　分析：只要能证明圆心到直线CD的距离等于⊙O的半径就可得结论．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：设计必修一数学(人教A版) 人教A版 题型：038

    如图所示，在梯形ABCD中，AB＝10，CD＝6，AD＝BC＝4，动点P从B点开始沿着折线BC、CD、DA前进至A，若P点运动的路程为x，△PAB的面积为y．

    (1)写出y＝f(x)的解析式，并求出函数的定义域；

    (2)画出函数的图象并求出函数的值域．

    查看答案和解析>>

    科目：高中数学 来源：全优设计必修五数学苏教版 苏教版 题型：044

    如图所示，在梯形ABCD中，AD∥BC，AB＝5，AC＝9，∠BCA＝30°，∠ADB＝45°．求BD的长度．

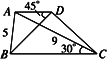
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，在梯形ABCD中，AB=10，CD=6，AD=BC=4，动点P从B点开始沿着折线BC，CD，DA前进至A，若P点运动的路程为x，△PAB的面积为y.

    (1)写出y=f(x)的解析式，指出函数的定义域；

    (2)画出函数的图像并求出函数的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）如图所示，在梯形ABCD中，AB∥CD，对角线AC和BD交于点O，E、F分别是AC和BD的中点，分别写出图中与、共线的向量，与相等的向量.

    （2）如下图所示，设O是正六边形ABCDEF的中心.在图里的向量中

    ①写出与相等的向量；

    ②写出与相等的向量；

    ③写出与共线的向量；

    ④写出与长度相等但方向相反的向量.

    查看答案和解析>>

    同步练习册答案