
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比到直线
的距离比到直线![]() 的距离小
的距离小![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,点
上任意一点,点![]() ,问是否存在垂直于
,问是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆是的弦长恒为定值?若存在,求出
为直径的圆是的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,直线
;(2)存在,直线![]() 的方程为
的方程为![]() ,定值为
,定值为![]()
【解析】
(1)根据题意可知,曲线![]() 上的点到点
上的点到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等,结合抛物线的定义,即可得到答案;
的距离相等,结合抛物线的定义,即可得到答案;
(2) 设直线![]() 方程为
方程为![]() ,
,![]() ,直线
,直线![]() 与以
与以![]() 为直径的圆的交点为
为直径的圆的交点为![]() ,
,![]() ,因为直线
,因为直线![]() 垂直于
垂直于![]() 轴,故弦长为
轴,故弦长为![]() ,因此根据圆的直径式方程写出以
,因此根据圆的直径式方程写出以![]() 为直径的圆的方程将
为直径的圆的方程将![]() 代入,利用根与系数关系求出
代入,利用根与系数关系求出![]() ,
,![]() 代入弦长
代入弦长![]() ,可求得
,可求得![]() ,令
,令![]() 即可得到答案.
即可得到答案.
(1)依题意得,曲线![]() 上的点到点
上的点到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
所以曲线![]() 的方程为:
的方程为:![]() .
.
(2)假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,
,![]() ,
,
则以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
将直线方程![]() 代入,得
代入,得![]() ,
,
则![]() .
.
设直线![]() 与以
与以![]() 为直径的圆的交点为
为直径的圆的交点为![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
于是有![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 为定值.
为定值.
故满足条件的直线![]() 存在,其方程为
存在,其方程为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为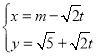 (其中
(其中![]() 为参数,
为参数,![]() ).以坐标原点
).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 被
被![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求实数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:
①若“![]() 或
或![]() ”为假命题,则
”为假命题,则![]() 均为假命题;
均为假命题;
②命题“若![]() 且
且![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() 且
且![]() ,则
,则![]() ”;
”;
③若![]() 是实数,则“
是实数,则“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
④命题“若![]() 则
则![]() ”的逆否命题为真命题.
”的逆否命题为真命题.
其中正确命题的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
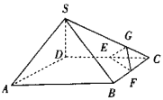
求证:(1)直线![]() 平面EFG;
平面EFG;
(2)直线![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
设函数![]()
(Ⅰ)若![]() 是函数
是函数![]() 的极值点,1和
的极值点,1和![]() 是
是![]() 的两个不同零点,且
的两个不同零点,且![]()
且![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若对任意![]() , 都存在
, 都存在![]() (
(![]() 为自然对数的底数),使得
为自然对数的底数),使得![]()
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
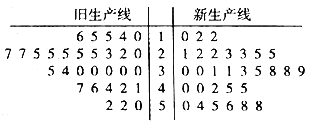
【题目】近几年,我国鲜切花产业得到了快速发展,相关部门制定了鲜切花产品行业等级标准,统一使用综合指标值![]() 进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
综合指标 |
|
|
|
质量等级 | 三级 | 二级 | 一级 |
(Ⅰ)根据茎叶图比较两条生产线加工的产品的综合指标值的平均值及分散程度(直接给出结论即可);
(Ⅱ)若从等级为三级的样品中随机选取3个进行生产流程调查,其中来自新型生产线的样品个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)根据该花卉生产基地的生产记录,原有生产线加工的产品的单件平均利润为4元,产品的销售率(某等级产品的销量与产量的比值)及产品售价如下表:
三级花 | 二级花 | 一级花 | |
销售率 |
|
|
|
单件售价 | 12元 | 16元 | 20元 |
预计该新型生产线加工的鲜切花单件产品的成本为span>10元,日产量3000件.因为鲜切花产品的保鲜特点,未售出的产品统一按原售价的50%全部处理完.如果仅从单件产品利润的角度考虑,该生产基地是否需要引进该新型生产线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,焦距为2,离心率
,焦距为2,离心率![]() 为
为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作圆
作圆![]() 的切线,切点分别为
的切线,切点分别为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com