
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为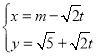 (其中
(其中![]() 为参数,
为参数,![]() ).以坐标原点
).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 被
被![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求实数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从秦朝统一全国币制到清朝末年,圆形方孔铜钱(简称“孔方兄”)是我国使用时间长达两千多年的货币.如图1,这是一枚清朝同治年间的铜钱,其边框是由大小不等的两同心圆围成的,内嵌正方形孔的中心与同心圆圆心重合,正方形外部,圆框内部刻有四个字“同治重宝”.某模具厂计划仿制这样的铜钱作为纪念品,其小圆内部图纸设计如图2所示,小圆直径1厘米,内嵌一个大正方形孔,四周是四个全等的小正方形(边长比孔的边长小),每个正方形有两个顶点在圆周上,另两个顶点在孔边上,四个小正方形内用于刻铜钱上的字.设![]() ,五个正方形的面积和为
,五个正方形的面积和为![]() .
.
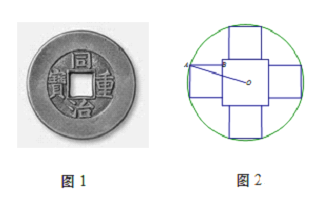
(1)求面积![]() 关于
关于![]() 的函数表达式,并求
的函数表达式,并求![]() 的范围;
的范围;
(2)求面积![]() 最小值.
最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部队在一次军演中要先后执行六项不同的任务,要求是:任务A必须排在前三项执行,且执行任务A之后需立即执行任务E,任务B、任务C不能相邻,则不同的执行方案共有( )
A. 36种B. 44种C. 48种D. 54种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 的底面
的底面![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]()

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在指出点
,若存在指出点![]() 的位置,若不存在请说明理由.
的位置,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于曲线![]() ,给出下列三个结论:
,给出下列三个结论:
① 曲线![]() 关于原点对称,但不关于
关于原点对称,但不关于![]() 轴、
轴、![]() 轴对称;
轴对称;
② 曲线![]() 恰好经过4个整点(即横、纵坐标均为整数的点);
恰好经过4个整点(即横、纵坐标均为整数的点);
③ 曲线![]() 上任意一点到原点的距离都不大于
上任意一点到原点的距离都不大于![]() .
.
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中不正确的是( )
A.设![]() 为直线,
为直线,![]() 为平面,且
为平面,且![]() ;则“
;则“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B.设随机变量![]() ,若
,若![]() ,则
,则![]()
C.若不等式![]() (
(![]() )恒成立,则
)恒成立,则![]() 的取值范围是
的取值范围是![]()
D.已知直线![]() 经过点
经过点![]() ,则
,则![]() 的取值范围是
的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雷达图(Radar Chart),又可称为戴布拉图、蜘蛛网图(Spider Chart),原先是财务分析报表的一种,现可用于对研究对象的多维分析.图为甲、乙两人在五个方面的评价值的雷达图,则下列说法不正确的是( )
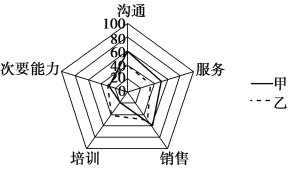
A.甲、乙两人在次要能力方面的表现基本相同
B.甲在沟通、服务、销售三个方面的表现优于乙
C.在培训与销售两个方面上,甲的综合表现优于乙
D.甲在这五个方面的综合表现优于乙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比到直线
的距离比到直线![]() 的距离小
的距离小![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,点
上任意一点,点![]() ,问是否存在垂直于
,问是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆是的弦长恒为定值?若存在,求出
为直径的圆是的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com