
【题目】设函数f(x)=asinωx+bcosωx(ω>0)的定义域为R,最小正周期为π,且对任意实数x,恒有![]() 成立.
成立.

(1)求实数a和b的值;
(2)作出函数f(x)在区间(0,π)上的大致图象;
(3)若两相异实数x1、x2∈(0,π),且满足f(x1)=f(x2),求f(x1+x2)的值.
【答案】(1)a=2,b=2![]() .(2)见解析 (3)f(x1+x2)=2
.(2)见解析 (3)f(x1+x2)=2![]() .
.
【解析】
(1)将f(x)=asinωx+bcosωx化为f(x)![]() sin(ωx+φ),由题意可得
sin(ωx+φ),由题意可得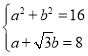 ,从而可求得a和b的值;
,从而可求得a和b的值;
(2)由f(x)=4sin(2x![]() )利用五点作图法即可作出其大致图象;
)利用五点作图法即可作出其大致图象;
(3)当0<x1<x2![]() 时,x1+x2
时,x1+x2![]() ,当
,当![]() x1<x2<π时,x1+x2
x1<x2<π时,x1+x2![]() ,从而可求得f(x1+x2)的值.
,从而可求得f(x1+x2)的值.
解(1)∵f(x)=asinωx+bcosωx![]() sin(ωx+φ)(ω>0),
sin(ωx+φ)(ω>0),
又f(x)≤f(![]() )=4恒成立,
)=4恒成立,
∴![]() 4,即a2+b2=16.…①
4,即a2+b2=16.…①
∵f(x)的最小正周期为π,
∴ω![]() 2,
2,
即f(x)=asin2x+bcos2x(ω>0).
又f(x)max=f(![]() )=4,
)=4,
∴asin![]() bcos
bcos![]() 4,
4,
即a![]() b=8.…②
b=8.…②
由①、②解得a=2,b=2![]() .
.
(2)由(1)知f(x)=2sin2x+2![]() cos2x=4sin(2x
cos2x=4sin(2x![]() ).
).
∵0<x<π,
∴![]() 2x
2x![]() ,列表如下:
,列表如下:
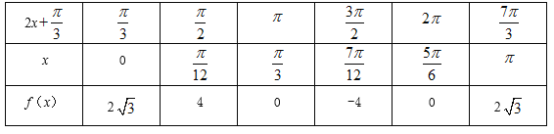
∴函数f(x)的图象如图所示:
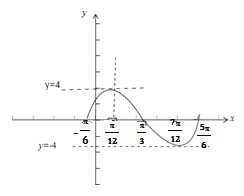
(3)∵f(x1)=f(x2),由f(x)=4sin(2x![]() )知,f(0)=f(
)知,f(0)=f(![]() )=2
)=2![]() ,
,
如图:
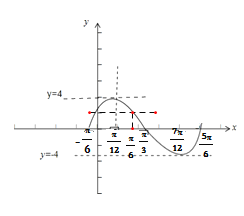
∴当0<x1<x2![]() 时,x1+x2=2
时,x1+x2=2![]() ,
,
∴f(x1+x2)=f(![]() )=4
)=4![]() 2
2![]() ;
;
当![]() x1<x2<π时,x1+x2=2
x1<x2<π时,x1+x2=2![]() ,
,
∴f(x1+x2)=f(![]() )=4sin
)=4sin![]() 2
2![]()
综上,f(x1+x2)=2![]() .
.


科目:高中数学 来源: 题型:
【题目】对任意实数![]() ,定义函数
,定义函数![]() ,已知函数
,已知函数![]() ,
,![]() ,记
,记![]() .
.
(1)若对于任意实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,且
,且![]() ,求使得等式
,求使得等式![]() 成立的
成立的![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答下列各题:
(1)已知扇形的周长为10cm,面积为4cm2,求扇形圆心角的弧度数.
(2)已知一扇形的圆心角是72°,半径等于20cm,求扇形的面积.
(3)已知一扇形的周长为40cm,求它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初始溶液含杂质2%,每过滤一次可使杂质含量减少![]() .
.
(1)写出杂质含量y与过滤次数n的函数关系式;
(2)过滤7次后的杂质含量是多少?过滤8次后的杂质含量是多少?至少应过滤几次才能使产品达到市场要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=tan(ωx+φ)(ω>0,0<φ<![]() ),已知函数y=f(x)的图象与x轴相邻两个交点的距离为
),已知函数y=f(x)的图象与x轴相邻两个交点的距离为![]() ,且图象关于点M(-
,且图象关于点M(-![]() ,0)对称.
,0)对称.
(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)求不等式-1≤f(x)≤![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com