
| A. | (1,$\sqrt{e}$) | B. | ($\sqrt{e}$,e) | C. | (e,+∞) | D. | ($\sqrt{e}$,+∞) |
分析 令b=${e}^{\frac{1}{m}}$>1,则y=mlnx=$lo{g}_{{e}^{\frac{1}{m}}}x$=logbx;y=$({e}^{\frac{1}{m}})^{x}$=bx,即函数y=mlnx(m>0)与y=${e}^{\frac{x}{m}}$ 互为反函数,且为增函数,两函数图形关于直线y=x对称,故其有两个交点等价于y=logbx 与 y=x有两个交点,即函数f(x)=logbx-x 有两个零点.
解答 解:令b=${e}^{\frac{1}{m}}$>1,则y=mlnx=$lo{g}_{{e}^{\frac{1}{m}}}x$=logbx;
y=$({e}^{\frac{1}{m}})^{x}$=bx,即函数y=mlnx(m>0)与y=${e}^{\frac{x}{m}}$ 互为反函数,且为增函数,
两函数图形关于直线y=x对称,故其有两个交点等价于y=logbx 与 y=x有两个交点,
即函数f(x)=logbx-x 有两个零点,
由f'(x)=$\frac{1}{x}(lo{g}_{b}e-x)$,
当0<x<logbe时,f'(x)>0;当x>logbe 时,f'(x)<0;
故f(x)max=f(logbe),所以f(logbe)>0;
即:logb(logbe)>logbe⇒$lo{g}_{b}e\\;>\\;e$>e;
⇒e>be⇒e>${e}^{\frac{e}{m}}$;
解得:m>e;
故选:C
点评 本题主要考查了反函数,方程根与图形交点问题以及转化思想的应用,属中等题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
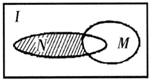 设全集I是实数集R,M={x|x≥3}与N={x|$\frac{x-3}{x-1}$≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|$\frac{x-3}{x-1}$≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com