
已知函数f(x)=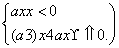 满足对任意x1≠x2,都有
满足对任意x1≠x2,都有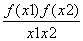 >0成立,则a的取值范围是
>0成立,则a的取值范围是
( )
A.(0,3) B.(1,3)
C. (0,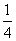 ] D.(3, +∞)
] D.(3, +∞)
科目:高中数学 来源: 题型:
若定义域为R的奇函数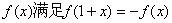 ,则下列结论:
,则下列结论:
①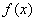 的图象关于点
的图象关于点 对称;
对称;
②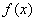 的图象关于直线
的图象关于直线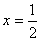 对称;
对称;
③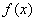 是周期函数,且2个它的一个周期;
是周期函数,且2个它的一个周期;
④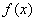 在区间(—1,1)上是单调函数,其中正确结论的序号是 。(填上你认为所有正确结论的序号)
在区间(—1,1)上是单调函数,其中正确结论的序号是 。(填上你认为所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
在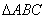 中,
中,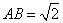 ,
, ,
,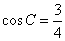 .
.
(1)求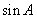 的值;
的值;
(2)求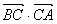 的值.
的值.
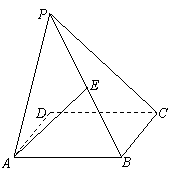 20.本大题满分12分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD = AB = a,E是PB的中点,F为AD中点.
20.本大题满分12分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD = AB = a,E是PB的中点,F为AD中点.
(1)求异面直线PD、AE所成的角;
(2)求证:EF⊥平面PBC.
(3)求二面角F-PC-E的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com