
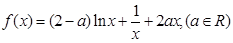
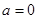 时,求
时,求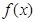 的极值;
的极值;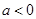 时,求
时,求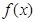 的单调区间.
的单调区间.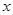 =
=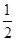 时,
时, 极小值=
极小值=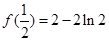 ,无极大值;
,无极大值;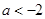 时,
时, 的单调递减区间为
的单调递减区间为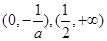
 的单调递增区间为
的单调递增区间为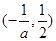
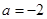 时,
时, 的单调递减区间为
的单调递减区间为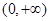
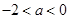 时,
时, 的单调递减区间为
的单调递减区间为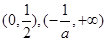
 的单调递增区间为
的单调递增区间为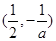 。
。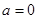 时,
时,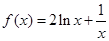 ,求导数研究单调性即可求出极值;(2)当
,求导数研究单调性即可求出极值;(2)当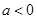 时,
时,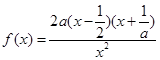 ,讨论
,讨论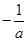 与
与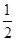 的大小可求出单调区间.
的大小可求出单调区间.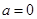 时,
时,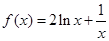
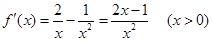 ……………………………2分
……………………………2分 |  |  | 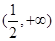 |
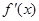 | - | 0 | + |
 | 单调递减 | 极小值 | 单调递增 |
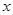 =
=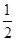 时,
时, 极小值=
极小值=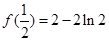 ,无极大值…………………………5分
,无极大值…………………………5分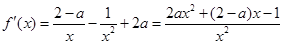
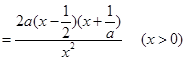 …………………………………………6分
…………………………………………6分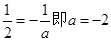 时,
时,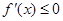 恒成立.
恒成立. 的单调递减区间为
的单调递减区间为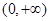 ………………………………7分
………………………………7分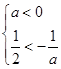 即
即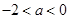 时
时 的单调递减区间为
的单调递减区间为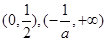
 的单调递增区间为
的单调递增区间为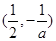 ……………………………9分
……………………………9分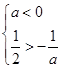 即
即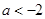 时,
时, 的单调递减区间为
的单调递减区间为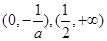
 的单调递增区间为
的单调递增区间为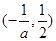 …………………………11分
…………………………11分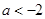 时,
时, 的单调递减区间为
的单调递减区间为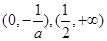
 的单调递增区间为
的单调递增区间为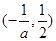
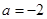 时,
时, 的单调递减区间为
的单调递减区间为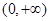
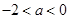 时,
时, 的单调递减区间为
的单调递减区间为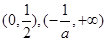
 的单调递增区间为
的单调递增区间为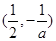 ……………………12分
……………………12分

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源:不详 题型:单选题

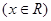 ,给出下列命题:①
,给出下列命题:①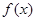 必是偶函数;②当
必是偶函数;②当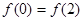 时,
时,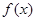 的图象关于直线
的图象关于直线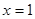 对称;③若
对称;③若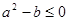 ,则
,则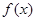 在区间
在区间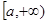 上是增函数;④
上是增函数;④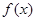 有最大值
有最大值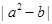 . 其中正确的命题序号是( )
. 其中正确的命题序号是( )| A.③ | B.②③ | C.②④ | D.①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com