
| A. | 该地区这次考试的数学平均数为88 | |
| B. | 该地区这次考试的数学标准差为10 | |
| C. | 分数在110分以上的人数和分数在60分以下的人数相同 | |
| D. | 分数在120分以上的人数和分数在56分以下的人数相同 |
分析 根据数学成绩符合正态分布和所给的函数式,得到这组数据的均值和标准差,判断出前两个选项的正误,根据数据的对称性判断出后面两个选项的正误.
解答 解:∵数学成绩服从正态分布,
其密度函数为f(x)=$\frac{1}{\sqrt{2π}•10}$e${\;}^{\frac{-(x-88)^{2}}{200}}$(x∈R),
∴μ=88,2σ2=200,
∴μ=88,σ=10,
∴这次考试的数学平均成绩是88,故A正确,
这次考试的数学标准差是10,故B正确,
∵正态曲线关于x=88对称,
∴在110分以上的人数和60分以下的人数不相同,故C正确,
分数在120以上的和分数在56分以下的相同,故D正确,
故选:D.
点评 本题考查正态分布曲线的特点及其曲线所表示的意义,考查曲线的对称性,考查密度函数的结构,本题是一个基础题.


科目:高中数学 来源: 题型:选择题
| A. | 39 | B. | 42 | C. | 48 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,该茎叶图表示的是北方图书城某台自动售书机连续15天的售书数量(单位:本),图中的数字7表示的意义是这台自动售书机在这15天中某天的售书数量为( )
如图,该茎叶图表示的是北方图书城某台自动售书机连续15天的售书数量(单位:本),图中的数字7表示的意义是这台自动售书机在这15天中某天的售书数量为( )| A. | 7本 | B. | 37本 | C. | 27本 | D. | 2337本 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:选择题
若函数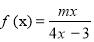
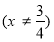 在定义域内恒有
在定义域内恒有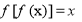 ,则
,则 的值等于( )
的值等于( )
A. 3 B.  C. -
C. -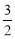 D. -3
D. -3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com