
【题目】抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点.
两点.
(1)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)若线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于
轴于![]() ,求证:
,求证:![]() ;
;
(3)若直线![]() 的斜率依次为
的斜率依次为![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,线段
,…,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点依次为
轴的交点依次为![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,求
,…,求![]() .
.
【答案】(1)k∈(﹣1,0)∪(0,1);(2)见解析(3)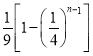
【解析】
(1)求得抛物线的准线方程,可得M的坐标和直线l的方程,联立抛物线方程,运用判别式大于0,即可得到所求范围;
(2)设A(x1,y1),B(x2,y2),运用韦达定理和中点坐标公式,以及两直线垂直的条件:斜率之积为﹣1,可得AB的垂直平分线方程,可令y=0,求得x,即可得证;
(3)设Nm(xm,0),求得![]() ,所以
,所以![]() ,由等比数列的求和公式,即可得到所求和.
,由等比数列的求和公式,即可得到所求和.
(1)抛物线y2=2x的准线为x![]() ,
,
![]() ,设l:
,设l:![]() ,
,
联立直线与抛物线的方程: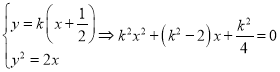 (*).
(*).
因为l交抛物线于两点,所以k≠0且二次方程(*)根的判别式△>0,
即(k2﹣2)2﹣k4>0,
解得k∈(﹣1,0)∪(0,1);
(2)证明:设A(x1,y1),B(x2,y2),
由韦达定理可得![]() ,
,![]() ,
,
所以AB中点的坐标为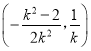 ,
,
所以AB中垂线方程为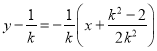 ,
,
令y=0,可得![]() .
.
(3)设Nm(xm,0),由直线l的斜率依次为![]() ,
,
可得xm![]() ,
,
则![]() ,
,
所以![]() ,
,
![]() (
(![]() )
)
![]()
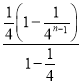 ,
,
所以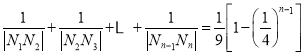 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,某小区为美化环境,准备在小区内的草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数![]() 的图象的一部分,后一段DBC是函数
的图象的一部分,后一段DBC是函数![]() 的图象,图象的最高点为
的图象,图象的最高点为 ,且
,且![]() ,垂足为点F.
,垂足为点F.

(1)求函数![]() 的解析式;
的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为![]() ,点E在OC上,求儿童乐园的面积.
,点E在OC上,求儿童乐园的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,
,![]() 为
为![]() 右支上的动点(非顶点),
右支上的动点(非顶点),![]() 为
为![]() 的内心.当
的内心.当![]() 变化时,
变化时,![]() 的轨迹为( )
的轨迹为( )
A.直线的一部分B.椭圆的一部分
C.双曲线的一部分D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市政府招商引资,为吸引外商,决定第一个月产品免税,某外资厂该第一个月A型产品出厂价为每件10元,月销售量为6万件;第二个月,当地政府开始对该商品征收税率为![]() ,即销售1元要征收
,即销售1元要征收![]() 元)的税收,于是该产品的出厂价就上升到每件
元)的税收,于是该产品的出厂价就上升到每件![]() 元,预计月销售量将减少p万件.
元,预计月销售量将减少p万件.
(1)将第二个月政府对该商品征收的税收y(万元)表示成p的函数,并指出这个函数的定义域;
(2)要使第二个月该厂的税收不少于1万元,则p的范围是多少?
(3)在第(2)问的前提下,要让厂家本月获得最大销售金额,则p应为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() 与
与![]() 轴相切.
轴相切.
(1)求![]() 的值;
的值;
(2)求圆M在![]() 轴上截得的弦长;
轴上截得的弦长;
(3)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作直线
作直线![]() 与圆M相切,
与圆M相切,![]() 为切点,求四边形
为切点,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)先将圆的一般方程化成标准方程,利用直线和圆相切进行求解;(2) 令![]() ,得到关于
,得到关于![]() 的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
试题解析:(1) ![]() ∵圆M:
∵圆M:![]() 与
与![]() 轴相切
轴相切
∴![]() ∴
∴![]()
(2) 令![]() ,则
,则![]() ∴
∴![]()
∴![]()
(3) ![]()
∵![]() 的最小值等于点
的最小值等于点![]() 到直线
到直线![]() 的距离,
的距离,
∴![]() ∴
∴![]()
∴四边形![]() 面积的最小值为
面积的最小值为![]() .
.
【题型】解答题
【结束】
20
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,且圆
,且圆![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,设直线
两点,设直线![]() 的方程为
的方程为![]() .
.

(1)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(2)已知直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点.
两点.
(ⅰ)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(ⅱ)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
, ![]() ,
,
是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com