
【题目】已知过点M( ![]() ,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且
,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且 ![]() =﹣3,其中O为坐标原点.
=﹣3,其中O为坐标原点.
(1)求p的值;
(2)当|AM|+4|BM|最小时,求直线l的方程.
【答案】
(1)解:设A(x1,y1),Bx2,y2),直线l:x=my+ ![]() ,
,
代入抛物线方程,消去x,得,y2﹣2pmy﹣p2=0,
y1+y2=2pm,y1y2=﹣p2,
由于 ![]() =﹣3,即x1x2+y1y2=﹣3,
=﹣3,即x1x2+y1y2=﹣3,
x1x2= ![]() =
= ![]() ,
,
即有 ![]() ﹣p2=﹣3,解得,p=2
﹣p2=﹣3,解得,p=2
(2)解:由抛物线的定义,可得,|AM|=x1+1,|BM|=x2+1,
则|AM|+4|BM|=x1+4x2+5 ![]() +5=9,
+5=9,
当且仅当x1=4x2时取得最小值9.
由于x1x2=1,则解得,x2= ![]() (负的舍去),
(负的舍去),
代入抛物线方程y2=4x,解得,y2= ![]() ,即有B(
,即有B( ![]() ),
),
将B的坐标代入直线x=my+1,得m= ![]() .
.
则直线l:x= ![]() y+1,即有4x+
y+1,即有4x+ ![]() y﹣4=0或4x﹣
y﹣4=0或4x﹣ ![]() y﹣4=0
y﹣4=0
【解析】(1)设A(x1 , y1),Bx2 , y2),直线l:x=my+ ![]() ,代入抛物线方程,运用韦达定理,及平面向量的数量积的坐标表示,即可得到p=2;(2)运用抛物线的定义,及均值不等式,即可得到最小值9,注意等号成立的条件,求得B的坐标,代入直线方程,求得m,即可得到直线l的方程.
,代入抛物线方程,运用韦达定理,及平面向量的数量积的坐标表示,即可得到p=2;(2)运用抛物线的定义,及均值不等式,即可得到最小值9,注意等号成立的条件,求得B的坐标,代入直线方程,求得m,即可得到直线l的方程.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】设F(x)=f(x)+f(﹣x)在区间 ![]() 是单调递减函数,将F(x)的图象按向量
是单调递减函数,将F(x)的图象按向量 ![]() 平移后得到函数G(x)的图象,则G(x)的一个单调递增区间是( )
平移后得到函数G(x)的图象,则G(x)的一个单调递增区间是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=2sin(3x﹣ ![]() ),有下列命题:①其表达式可改写为y=2cos(3x﹣
),有下列命题:①其表达式可改写为y=2cos(3x﹣ ![]() );②y=f(x)的最小正周期为
);②y=f(x)的最小正周期为 ![]() ;③y=f(x)在区间(
;③y=f(x)在区间( ![]() ,
, ![]() )上是增函数;④将函数y=2sin3x的图象上所有点向左平行移动
)上是增函数;④将函数y=2sin3x的图象上所有点向左平行移动 ![]() 个单位长度就得到函数y=f(x)的图象.其中正确的命题的序号是(注:将你认为正确的命题序号都填上).
个单位长度就得到函数y=f(x)的图象.其中正确的命题的序号是(注:将你认为正确的命题序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条宽为![]() 的两平行河岸有村庄
的两平行河岸有村庄![]() 和供电站
和供电站![]() ,村庄
,村庄![]() 与
与![]() 的直线距离都是
的直线距离都是![]() ,
, ![]() 与河岸垂直,垂足为
与河岸垂直,垂足为![]() 现要修建电缆,从供电站
现要修建电缆,从供电站![]() 向村庄
向村庄![]() 供电.修建地下电缆、水下电缆的费用分别是
供电.修建地下电缆、水下电缆的费用分别是![]() 万元
万元![]() 、
、![]() 万元
万元![]() .
.
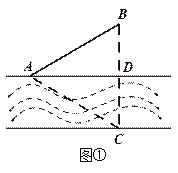
(1) 如图①,已知村庄![]() 与
与![]() 原来铺设有电缆
原来铺设有电缆![]() ,现先从
,现先从![]() 处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
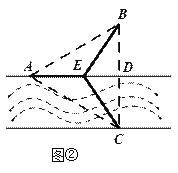
(2) 如图②,点![]() 在线段
在线段![]() 上,且铺设电缆的线路为
上,且铺设电缆的线路为![]() .若
.若![]() ,试用
,试用![]() 表示出总施工费用
表示出总施工费用![]() (万元)的解析式,并求
(万元)的解析式,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com