
【题目】一条宽为![]() 的两平行河岸有村庄
的两平行河岸有村庄![]() 和供电站
和供电站![]() ,村庄
,村庄![]() 与
与![]() 的直线距离都是
的直线距离都是![]() ,
, ![]() 与河岸垂直,垂足为
与河岸垂直,垂足为![]() 现要修建电缆,从供电站
现要修建电缆,从供电站![]() 向村庄
向村庄![]() 供电.修建地下电缆、水下电缆的费用分别是
供电.修建地下电缆、水下电缆的费用分别是![]() 万元
万元![]() 、
、![]() 万元
万元![]() .
.
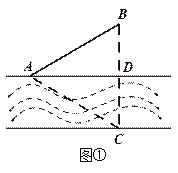
(1) 如图①,已知村庄![]() 与
与![]() 原来铺设有电缆
原来铺设有电缆![]() ,现先从
,现先从![]() 处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
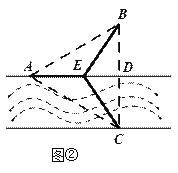
(2) 如图②,点![]() 在线段
在线段![]() 上,且铺设电缆的线路为
上,且铺设电缆的线路为![]() .若
.若![]() ,试用
,试用![]() 表示出总施工费用
表示出总施工费用![]() (万元)的解析式,并求
(万元)的解析式,并求![]() 的最小值.
的最小值.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知过点M( ![]() ,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且
,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且 ![]() =﹣3,其中O为坐标原点.
=﹣3,其中O为坐标原点.
(1)求p的值;
(2)当|AM|+4|BM|最小时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线x2﹣ ![]() =1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
A.10
B.13
C.16
D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥S﹣ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: ①异面直线SB与AC所成的角为90°;
②直线SB⊥平面ABC;
③面SBC⊥面SAC;
④点C到平面SAB的距离是 ![]() .
.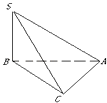
其中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a5=9,a7=13,等比数列{bn}的通项公式bn=2n﹣1 , n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an+bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
(I)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB= ![]() AC=2
AC=2 ![]() ,AB=BC,求二面角F﹣BC﹣A的余弦值.
,AB=BC,求二面角F﹣BC﹣A的余弦值.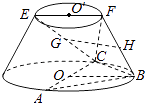
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x2﹣kx﹣8,x∈[1,5].
(1)当k=12时,求f(x)的值域;
(2)若函数f(x)具有单调性,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com