
【题目】设函数f(x)=![]() (a>0且a≠1)是定义域为R的奇函数.
(a>0且a≠1)是定义域为R的奇函数.
(Ⅰ)若f(1)>0,试求不等式f(x2+2x)+f(x-4)>0的解集;
(Ⅱ)若f(1)=![]() ,且g(x)=a2x+a-2x-4f(x),求g(x)在[1,+∞)上的最小值.
,且g(x)=a2x+a-2x-4f(x),求g(x)在[1,+∞)上的最小值.
【答案】(1){x|x>1,或x<-4}.(2)最小值-2.
【解析】试题分析:(1)(2)
试题解析:∵f(x)是定义域为R的奇函数,∴f(0)=0,∴k-1=0,即k=1,经检验k=1合题意.
(Ⅰ)∵f(1)>0,∴a-![]() >0,又a>0且a≠1,∴a>1,f(x)=ax-a-x,∴f(x)在R上为增函数.
>0,又a>0且a≠1,∴a>1,f(x)=ax-a-x,∴f(x)在R上为增函数.
原不等式可化为f(x2+2x)>f(4-x),∴x2+2x>4-x,即x2+3x-4>0,∴x>1或x<-4,
∴不等式的解集为{x|x>1,或x<-4}.
(Ⅱ)∵f(1)=![]() ,∴a-
,∴a-![]() =
=![]() ,即2a2-3a-2=0,∴a=2或a=-
,即2a2-3a-2=0,∴a=2或a=-![]() (舍去),
(舍去),
∴g(x)=22x+2-2x-4(2x-2-x)=(2x-2-x)2-4(2x-2-x)+2.
令t=2x-2-x(x≥1),则t是[1,+∞)上的增函数,即t≥![]() ,
,
∴原函数变为w(t)=t2-4t+2=(t-2)2-2,∴当t=2时,w(t)min=-2,此时x=log2(1+![]() ).
).
即g(x)在x=log2(1+![]() )时取得最小值-2.
)时取得最小值-2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-![]() ,0),且过点D(2,0).
,0),且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点A(1,![]() ),若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
),若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P到两点(0,-![]() ),(0,
),(0,![]() )的距离之和等于4,设点P的轨迹为C.
)的距离之和等于4,设点P的轨迹为C.
(1)写出C的方程;
(2)设直线y=kx+1与C交于A、B两点,k为何值时![]()
![]()
![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知![]() +
+![]() =1(a>>0)点A(1,
=1(a>>0)点A(1,![]() )是离心率为
)是离心率为![]() 的椭圆C:上的一点,斜率为
的椭圆C:上的一点,斜率为![]() 的直线BD交椭圆C于B、D两点,且A、B、D三点不重合.
的直线BD交椭圆C于B、D两点,且A、B、D三点不重合.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求△ABD面积的最大值;
(Ⅲ)设直线AB、AD的斜率分别为k1 , k2 , 试问:是否存在实数λ,使得k1+λk2=0成立?若存在,求出λ的值;否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.
(Ⅰ)若a=b,求cosB;
(Ⅱ)设B=90°,且a=![]() , 求△ABC的面积.
, 求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司研究开发了一种新产品,生产这种新产品的年固定成本为150万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() (万元),
(万元), 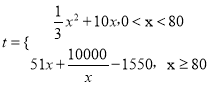 .每件产品售价为500元.该新产品在市场上供不应求可全部卖完.
.每件产品售价为500元.该新产品在市场上供不应求可全部卖完.
(Ⅰ)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)当年产量为多少千件时,该公司在这一新产品的生产中所获利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量主要受污染物排放量及大气扩散等因素的影响,某市环保监测站2014年10月连续10天(从左到右对应1号至10号)采集该市某地平均风速及空气中氧化物的日均浓度数据,制成散点图如图所示.
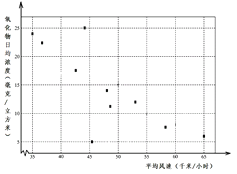
(Ⅰ)同学甲从这10天中随机抽取连续5天的一组数据,计算回归直线方程.试求连续5天的一组数据中恰好同时包含氧化物日均浓度最大与最小值的概率;
(Ⅱ)现有30名学生,每人任取5天数据,对应计算出30个不同的回归直线方程.已知30组数据中有包含氧化物日均浓度最值的有14组.现采用这30个回归方程对某一天平均风速下的氧化物日均浓度进行预测,若预测值与实测值差的绝对值小于2,则称之为“拟合效果好”,否则为“拟合效果不好”.根据以上信息完成下列2×2联表,并分析是否有95%以上的把握说拟合效果与选取数据是否包含氧化物日均浓度最值有关.
预测效果好 | 拟合效果不好 | 合计 | |
数据有包含最值 | 5 | ||
数据无包含最值 | 4 | ||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
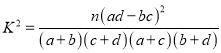 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点,求证: 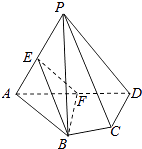
(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com