
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点,求证: 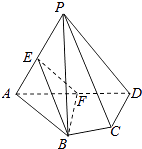
(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
【答案】
(1)证明:在△PAD中,因为E,F分别为AP,AD的中点,所以EF∥PD.
又因为EF不在平面PCD中,PD平面PCD
所以直线EF∥平面PCD.
(2)证明:连接BD.因为AB=AD,∠BAD=60°.
所以△ABD为正三角形.因为F是AD的中点,所以BF⊥AD.
因为平面PAD⊥平面ABCD,BF平面ABCD,
平面PAD∩平面ABCD=AD,所以BF⊥平面PAD.
又因为BF平面EBF,所以平面BEF⊥平面PAD.
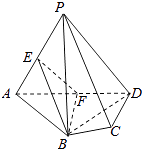
【解析】(1)要证直线EF∥平面PCD,只需证明EF∥PD,EF不在平面PCD中,PD平面PCD即可.(2)连接BD,证明BF⊥AD.说明平面PAD∩平面ABCD=AD,推出BF⊥平面PAD;然后证明平面BEF⊥平面PAD.
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() (a>0且a≠1)是定义域为R的奇函数.
(a>0且a≠1)是定义域为R的奇函数.
(Ⅰ)若f(1)>0,试求不等式f(x2+2x)+f(x-4)>0的解集;
(Ⅱ)若f(1)=![]() ,且g(x)=a2x+a-2x-4f(x),求g(x)在[1,+∞)上的最小值.
,且g(x)=a2x+a-2x-4f(x),求g(x)在[1,+∞)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,其前n项的和为Sn,且对任意的m,n∈N*,
都有(Sm+n+S1)2=4a2ma2n.
(1)求![]() 的值;
的值;
(2)求证:{an}为等比数列;
(3)已知数列{cn},{dn}满足|cn|=|dn|=an,p(p≥3)是给定的正整数,数列{cn},{dn}的前p项的和分别为Tp,Rp,且Tp=Rp,求证:对任意正整数k(1≤k≤p),ck=dk.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人上午7时乘船出发,以匀速![]() 海里/小时
海里/小时![]() 从
从![]() 港前往相距50海里的
港前往相距50海里的![]() 港,然后乘汽车以匀速
港,然后乘汽车以匀速![]() 千米/小时(
千米/小时(![]() )自
)自![]() 港前往相距
港前往相距![]() 千米的
千米的![]() 市,计划当天下午4到9时到达
市,计划当天下午4到9时到达![]() 市.设乘船和汽车的所要的时间分别为
市.设乘船和汽车的所要的时间分别为![]() 、
、![]() 小时,如果所需要的经费
小时,如果所需要的经费![]() (单位:元)
(单位:元)

(1)试用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() ;
;
(2)要使得所需经费![]() 最少,求
最少,求![]() 和
和![]() 的值,并求出此时的费用.
的值,并求出此时的费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
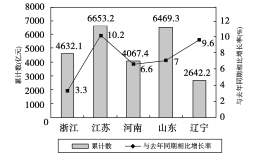
①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数y=f(x),若在其定义域内存在x0 , 使得x0f(x0)=1成立,则称x0为函数f(x)的“反比点”.下列函数中具有“反比点”的是
①f(x)=﹣2x+2![]() ; ②f(x)=sinx,x∈[0,2π];
; ②f(x)=sinx,x∈[0,2π];
③f(x)=x+![]() , x∈(0,+∞);④f(x)=ex; ⑤f(x)=﹣2lnx.
, x∈(0,+∞);④f(x)=ex; ⑤f(x)=﹣2lnx.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点(0,4),斜率为﹣1的直线与抛物线y2=2px(p>0)交于两点A、B,且弦|AB|的长度为4![]() .
.
(1)求p的值;
(2)求证:OA⊥OB(O为原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾天气对城市环境造成很大影响,按照国家环保部发布的标准:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米.某市环保部门加强了对空气质量的监测,抽取某居民区监测点的20天PM2.5的24小时平均浓度的监测数据,制成茎叶图,如图:
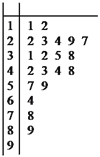
(Ⅰ)完成如下频率分布表,并在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
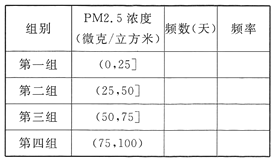
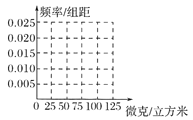
(Ⅱ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com