
【题目】已知函数![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 的单调区间.
的单调区间.
(![]() )当
)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
(![]() )在条件(
)在条件(![]() )下,当最小值为
)下,当最小值为![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时, ![]() 的单调区间为
的单调区间为![]() ,单调减区间是
,单调减区间是![]() ,当
,当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间是
,单调减区间是![]() ;当
;当![]() 时,
时, ![]() 的单调增区间是
的单调增区间是![]() ;当
;当![]() 时,
时, ![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,单调减区间是
,单调减区间是![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求出![]() ,分四种情况讨论
,分四种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)分三种情况讨论
的减区间;(2)分三种情况讨论![]() 的范围,分别利用导数研究函数的单调性,根据单调性可求得函数
的范围,分别利用导数研究函数的单调性,根据单调性可求得函数![]() 在区间
在区间![]() 上的最小值;(3)分三种情况讨论
上的最小值;(3)分三种情况讨论![]() 的范围,分别利用导数求出函数的最小值,排除不合题意的情况,即可筛选出符合题意的
的范围,分别利用导数求出函数的最小值,排除不合题意的情况,即可筛选出符合题意的![]() 的取值范围.
的取值范围.
试题解析:( ![]() )由函数
)由函数![]() 可知,
可知,
函数![]() 的定义域是
的定义域是![]() ,且
,且![]() ,
,
当![]() 时,
时, ![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,单调减区间是
,单调减区间是![]() ;
;
当![]() 时,令
时,令![]() 得
得![]() 或
或![]() ,
,
若![]() ,即
,即![]() ,则
,则![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递增,
上单调递增,
若![]() ,即
,即![]() ,则
,则![]() 和
和![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
若![]() ,即
,即![]() ,则
,则![]() 和
和![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
综上所述,当![]() 时,
时, ![]() 的单调区间为
的单调区间为![]() ,单调减区间是
,单调减区间是![]() ,
,
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间是
,单调减区间是![]() ;
;
当![]() 时,
时, ![]() 的单调增区间是
的单调增区间是![]() ;
;
当![]() 时,
时, ![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,单调减区间是
,单调减区间是![]() .
.
(![]() )由(
)由(![]() )可知,当
)可知,当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上的最小值是
上的最小值是![]() ,
,
当![]() 时,即
时,即![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 的最小值是
的最小值是![]() ,
,
综上所述,当![]() 时,
时, ![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上的最小值是
上的最小值是![]() .
.
(![]() )由(
)由(![]() )可知,当
)可知,当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上最小值是
上最小值是![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
综上,若![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,则
,则![]() ,
,
故![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( )

A. ![]() 的图象关于直线
的图象关于直线![]() 对称
对称
B. ![]() 的图象关于点
的图象关于点![]() 对称
对称
C. 将函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到函数
个单位得到函数![]() 的图象
的图象
D. 若方程![]() 在
在![]() 上有两个不相等的实数根,则实数
上有两个不相等的实数根,则实数![]() 的取值范围是
的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=(|x﹣2|+1)4,给出如下三个命题:①f(x+2)是偶函数;②f(x)在区间(﹣∞,2)上是减函数,在区间(2,+∞)上是增函数;③f(x)没有最小值.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位安排![]() 位员工在春节期间大年初一到初七值班,每人值班
位员工在春节期间大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有( )
位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:

(1)求网民消费金额![]() 的平均值和中位数
的平均值和中位数![]() ;
;
(2)把下表中空格里的数填上,能否有90%的把握认为网购消费与性别有关;


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
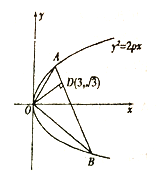
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率![]() ,点
,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
(2)若直线![]() 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com