Question

【题目】已知双曲线（b＞a＞0），O为坐标原点，离心率，点在双曲线上.

（1）求双曲线的方程；

（2）若直线与双曲线交于P、Q两点，且.求|OP|2+|OQ|2的最小值.

Answer 1

【答案】1 ； 2.

【解析】试题分析：

(Ⅰ) 由，可得，故双曲线方程为，代入点的坐标可得，由此可得双曲线方程． (Ⅱ)根据直线的斜率存在与否分两种情况求解．当斜率存在时，可根据一元二次方程根与系数的关系及两点间的距离公式求解即可．当斜率不存在时直接计算可得结果．

试题解析：

（1）由，可得，

∴，

∴ 双曲线方程为，

∵ 点在双曲线上，

∴，

解得 ，

∴ 双曲线的方程为．

（2）①当直线的斜率存在时，设直线的方程为，

由消去y整理得，

∵直线与双曲线交于两点，

∴．

设， ，

则，

由得到： ，

即，

∴，

化简得．

∴，

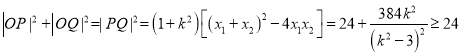当时上式取等号，且方程（*）有解．

②当直线的斜率不存在时，设直线的方程为，则有，

由可得，

可得，解得.

∴．

∴ ．

综上可得的最小值是24．