
【题目】选修4﹣5:不等式选讲
已知函数f(x)=|x+1|﹣|x|+a.
(1)若a=0,求不等式f(x)≥0的解集;
(2)若方程f(x)=x有三个不同的解,求a的取值范围.
【答案】
(1)解:若a=0,f(x)=|x+1|﹣|x|= 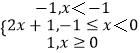 ,
,
∴当 x<﹣1时,不等式 即﹣1≥0,解得x∈.
当﹣1≤x<0时,不等式即 2x+1≥0,解得 x≥﹣ ![]() .综合可得﹣
.综合可得﹣ ![]() ≤x<0.
≤x<0.
当x≥0 时,不等式即 1≥0,恒成立,故不等式的解集为x≥0.
综上,不等式的解集为[﹣ ![]() ,+∞).
,+∞).
(2)解:设u(x)=|x+1|﹣|x|,则函数u(x)的图象和 y=x的图象如下图:
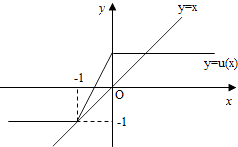
由题意易知,把函数y=u(x)的图象向下平移1个单位以内(不包括1个单位)与y=x的图象始终有3个交点,
从而﹣1<a<0.
【解析】(1)若a=0,则f(x)= 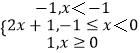 ,分 x<﹣1时、当﹣1≤x<0时、当x≥0 时,三种情况,分别求得不等式的解集,再取并集,即得所求.(2)设u(x)=|x+1|﹣|x|,由题意易知,把函数y=u(x)的图象向下平移1个单位以内(不包括1个单位)与y=x的图象始终有3个交点,从而求得a的范围.
,分 x<﹣1时、当﹣1≤x<0时、当x≥0 时,三种情况,分别求得不等式的解集,再取并集,即得所求.(2)设u(x)=|x+1|﹣|x|,由题意易知,把函数y=u(x)的图象向下平移1个单位以内(不包括1个单位)与y=x的图象始终有3个交点,从而求得a的范围.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x)=(|x﹣2|+1)4,给出如下三个命题:①f(x+2)是偶函数;②f(x)在区间(﹣∞,2)上是减函数,在区间(2,+∞)上是增函数;③f(x)没有最小值.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
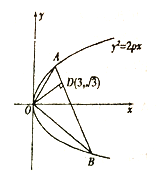
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某种商品在过去50天的销量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N),前30天价格为g(t)=![]() t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系式;
(2)求日销售额S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,其中a>﹣1.若f(x)在R上是增函数,则实数a的取值范围是( )
,其中a>﹣1.若f(x)在R上是增函数,则实数a的取值范围是( )
A.[e+1,+∞)
B.(e+1,+∞)
C.(e﹣1,+∞)
D.[e﹣1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率![]() ,点
,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
(2)若直线![]() 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程和离心率;
的方程和离心率;
(Ⅱ)设点![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 在
在![]() 轴的右侧,线段
轴的右侧,线段![]() 的垂直平分线
的垂直平分线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com