Question

已知关于x的方程x²+ax+b=0的两根均在区间（-1，1）内，则

a+b-2

a+1

的取值范围是

(-∞，

1

3

) ∪(3，+∞)

．

Answer 1

分析：由题意关于x的方程x²+ax+b=0的两根均在区间（-1，1）内，令f（x）=x²+ax+b，可得

f(1)＞0 f(-1)＞0 f(- a 2 )＜0 -1＜- a 2 ＜1

，即

1+a+b＞0 1-a+b＞0 - a2 4 +b＜0 -2＜a＜2

作出此不等式对应的区域，如图中阴影部分，不包括边界，由于

a+b-2

a+1

=1+

b-3

a+1

，而

b-3

a+1

可看作点P（-1，3）与阴影部分内一点（a，b）连线的斜率，由此问题转化为线性规划求范围问题，易解．

解答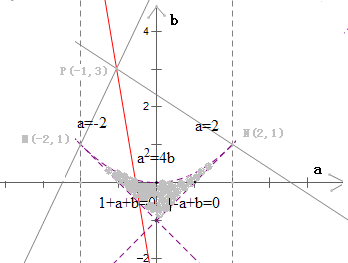：解：关于x的方程x²+ax+b=0的两根均在区间（-1，1）内，令f（x）=x²+ax+b
∴

f(1)＞0 f(-1)＞0 f(- a 2 )＜0 -1＜- a 2 ＜1

，即

1+a+b＞0 1-a+b＞0 - a2 4 +b＜0 -2＜a＜2

此不等式对应的区域图象如图阴影部分，不包括边界．
由于

a+b-2

a+1

=1+

b-3

a+1

，而

b-3

a+1

可看作点
P（-1，3）与阴影部分内一点（a，b）连线的斜率，如图红色线即为符合条件的直线
M，N两个点为边界处的点，由于kPM=

3-1

-1+2

=2，kPN=

3-1

-1-2

=-

2

3

，由图知

b-3

a+1

∈（2，+∞）∪（-∞，-

2

3

）
∴

a+b-2

a+1

=1+

b-3

a+1

∈(-∞，

1

3

) ∪(3，+∞)
故答案为(-∞，

1

3

) ∪(3，+∞)

点评：本题考查了简单线性的应用，一元二次方程的根的分布与系数的关系，正确解答本题，能分析出求

a+b-2

a+1

的取值范围是解题的关键，由于本题通过根的分布的知识得出的不等式组较复杂，不宜将求

a+b-2

a+1

的取值范围的问题转化为函数的值域求解，转化为线性规划知识求解是本题的难点也是重点，本题考查了转化的思想，数形结合的思想，考查转化化归的能力及数形结合解题的意识，综合性强，是能力型题