分析:(1)利用平面向量的数量积运算法则化简已知的等式左右两边,然后两边同时除以c化简后,再利用正弦定理变形,根据cosAcosB≠0,利用同角三角函数间的基本关系弦化切即可得到tanB=3tanA;
(2)由C为三角形的内角,及cosC的值,利用同角三角函数间的基本关系求出sinC的值,进而再利用同角三角函数间的基本关系弦化切求出tanC的值,由tanC的值,及三角形的内角和定理,利用诱导公式求出tan(A+B)的值,利用两角和与差的正切函数公式化简后,将tanB=3tanA代入,得到关于tanA的方程,求出方程的解得到tanA的值,再由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数.
解答:解:(1)∵
•
=3
•
,
∴cbcosA=3cacosB,即bcosA=3acosB,
由正弦定理
=
得:sinBcosA=3sinAcosB,
又0<A+B<π,∴cosA>0,cosB>0,
在等式两边同时除以cosAcosB,可得tanB=3tanA;
(2)∵cosC=
,0<C<π,
sinC=
=
,
∴tanC=2,
则tan[π-(A+B)]=2,即tan(A+B)=-2,
∴
=-2,
将tanB=3tanA代入得:
=-2,
整理得:3tan
2A-2tanA-1=0,即(tanA-1)(3tanA+1)=0,
解得:tanA=1或tanA=-
,
又coaA>0,∴tanA=1,
又A为三角形的内角,
则A=
.
点评:此题属于解三角形的题型,涉及的知识有:平面向量的数量积运算法则,正弦定理,同角三角函数间的基本关系,诱导公式,两角和与差的正切函数公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.



 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案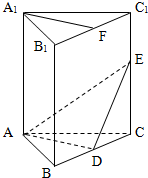 (2012•江苏)如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(2012•江苏)如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证: