
【题目】对于区间[a,b](a<b),若函数![]() 同时满足:①
同时满足:①![]() 在[a,b]上是单调函数,②函数
在[a,b]上是单调函数,②函数![]() 在[a,b]的值域是[a,b],则称区间[a,b]为函数
在[a,b]的值域是[a,b],则称区间[a,b]为函数![]() 的“保值”区间
的“保值”区间
(1)求函数![]() 的所有“保值”区间
的所有“保值”区间
(2)函数![]() 是否存在“保值”区间?若存在,求
是否存在“保值”区间?若存在,求![]() 的取值范围,若不存在,说明理由
的取值范围,若不存在,说明理由
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由已知中的保值区间的定义,结合函数![]() 的值域是
的值域是![]() ,可得
,可得![]() ,从而函数
,从而函数![]() 在区间
在区间![]() 上单调,列出方程组,可求解;
上单调,列出方程组,可求解;
(2)根据已知保值区间的定义,分函数![]() 在区间
在区间![]() 上单调递减和函数
上单调递减和函数![]() 在区间
在区间![]() 单调递增,两种情况分类讨论,即可得到答案.
单调递增,两种情况分类讨论,即可得到答案.
(1)因为函数![]() 的值域是
的值域是![]() ,且
,且![]() 在
在![]() 的最后综合讨论结果,
的最后综合讨论结果,
即可得到值域是![]() ,所以
,所以![]() ,所以
,所以![]() ,从而函数
,从而函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故有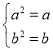 ,解得
,解得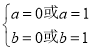 .
.
又![]() ,所以
,所以![]() .所以函数
.所以函数![]() 的“保值”区间为
的“保值”区间为![]() .
.
(2)若函数![]() 存在“保值”区间,则有:
存在“保值”区间,则有:
①若![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以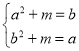 ,消去
,消去![]() 得
得![]() ,整理得
,整理得![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() .又
.又![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
②若![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以 ,消去
,消去![]() 得
得![]() ,整理得
,整理得![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
综合①、②得,函数![]() 存在“保值”区间,此时
存在“保值”区间,此时![]() 的取值范围是
的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,P点的极坐标为(3, ![]() ).曲线C的参数方程为ρ=2cos(θ﹣
).曲线C的参数方程为ρ=2cos(θ﹣ ![]() )(θ为参数).
)(θ为参数).
(Ⅰ)写出点P的直角坐标及曲线C的直角坐标方程;
(Ⅱ)若Q为曲线C上的动点,求PQ的中点M到直线l:2ρcosθ+4ρsinθ= ![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的各项均为正数,a1=1,前n项和为Sn.数列{bn}为等比数列,b1=1,且b2S2=6,b2+S3=8.
(1)求数列{an}与{bn}的通项公式;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A. (8,+∞) B. (8,9] C. [8,9] D. (0,8)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)已知函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)若函数f(x)的最小值是f(-1)=0,且c=1, F(x)=![]() 求F(2)+F(-2)的值;
求F(2)+F(-2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,点(an , an+1)在直线y=x+2上,且首项a1是方程3x2﹣4x+1=0的整数解.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{an}的前n项和为Sn , 等比数列{bn}中,b1=a1 , b2=a2 , 数列{bn}的前n项和为Tn , 当Tn≤Sn时,请直接写出n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探究函数![]() ,x∈(0,+∞)取最小值时x的值,列表如下:
,x∈(0,+∞)取最小值时x的值,列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题:
(1)函数![]() (x>0)在区间(0,2)上递减;函数
(x>0)在区间(0,2)上递减;函数![]() 在区间________上递增.当x=_________时,
在区间________上递增.当x=_________时,![]() _______.
_______.
(2)证明:函数![]() (x>0)在区间(O,2)上递减.
(x>0)在区间(O,2)上递减.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com