
实数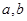 是分别从集合A={1,2,3,4}中随机抽取的元素,集合B=
是分别从集合A={1,2,3,4}中随机抽取的元素,集合B=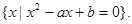
(1)写出使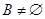 的所有实数对
的所有实数对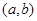
(2)求随机抽取的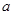 与
与 的值满足
的值满足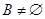 且
且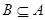 的概率.
的概率.
(1)(2,1)(3,1)(3,2)(4,1)(4,2)(4,3)(4,4);(2)P=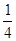 。
。
解析试题分析:(1)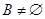 也就是
也就是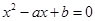 有根,因而可知
有根,因而可知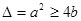 ,再结合a,b从集合A中取值可得满足条件的实数对
,再结合a,b从集合A中取值可得满足条件的实数对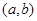 .
.
(2)根据(1)可知(a,b)共有16组,然后找出满足条件的有4组,根据古典概型概率计算公式计算即可.
(1)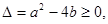 即
即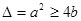 ,则B
,则B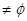 时
时
(a,b)是:(2,1)(3,1)(3,2)(4,1)(4,2)(4,3)(4,4)……6分
(2)(a,b)共有16组,其中满足条件有:(2,1)(3,2)(4,3)(4,4)4组,P=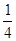 ……12分
……12分
考点:集合的定义及表示,集合间的包含关系,古典概型的概率问题.
点评:掌握集合的概念及其表示方法,以及集合之间的包含关系是解决本题的突破口,然后再计算概率时要注意本小题属于古典概型概率问题.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com