
(本小题满分12分)
定义在R上的偶函数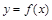 在
在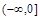 上递增,函数
上递增,函数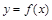 的一个零点为-
的一个零点为-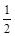 。
。
求满足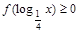 的x的取值集合.
的x的取值集合.
{x|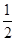 ≤x≤2}
≤x≤2}
解析试题分析: ∵-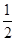 是函数的零点,∴
是函数的零点,∴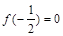 ,…………………………………1分
,…………………………………1分
∵ 为偶函数,∴
为偶函数,∴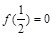 ,…………………………………2分
,…………………………………2分
∵ 在(-∞,0]上递增,
在(-∞,0]上递增,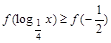 …………………………4分
…………………………4分
∴0≥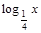 ≥-
≥-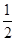 ,∴1≤x≤2,…………………………………7分
,∴1≤x≤2,…………………………………7分
∵ 为偶函数,∴
为偶函数,∴ 在[0,+∞)上单调减,…………………………………8分
在[0,+∞)上单调减,…………………………………8分
又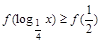 ,∴0≤
,∴0≤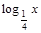 ≤
≤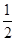 ,∴
,∴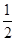 ≤x≤1,∴
≤x≤1,∴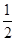 ≤x≤2.………………11分
≤x≤2.………………11分
故x的取值集合为{x|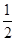 ≤x≤2}.…………………………………12分
≤x≤2}.…………………………………12分
考点:本试题考查了函数的零点以及对数不等式的求解运用。
点评:解决该试题的关键是利用函数的零点,转化为该数是方程的一个根,进而根据偶函数求解得到函数值为零的点,然后结合单调性来得到不等式的解集。属于中档题。 易错点是对数不等式的求解,忽略了单调性造成不等式符号的错误 。


科目:高中数学 来源: 题型:解答题
(本题12分)已知P: 且
且 ,已知Q:
,已知Q: 且
且 .
.
(Ⅰ)在区间(-4,4)上任取一个实数x,求命题“P且Q”为真的概率;
(Ⅱ)设在数对 中,
中, ,
, ,求“事件
,求“事件 ”发生的概率.
”发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com