在△ABC中,角B=45°,角B的对边b=2,若这样的三角形有且只有一解,则角A的对边a的取值范围为 .
【答案】
分析:由B的度数求出sinB的值,再由b的值,利用正弦定理得出a与sinA的关系式,同时由B的度数求出A+C的度数,再根据三角形只有一解,可得A只有一个值,根据正弦函数的图象与性质得到A的范围,且当A为直角时,也满足题意,进而由A的范围,求出正弦函数的值域,根据a与sinA的关系式,由正弦函数的值域即可可得出a的范围.
解答:解:∵B=45°,b=2,
根据正弦定理得:
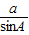
=
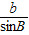
=2
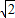
,
∴a=2
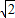
sinA,
又A+C=180°-45°=135°,且三角形只一解,可得A有一个值,
∴0<A≤45°,
又A=90°时,三角形也只有一解,
∴0<sinA≤
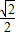
,或sinA=1,
又a=2
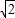
sinA,
∴a的取值范围为(0,2]∪{2
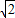
}.
故答案为:(0,2]∪{2

}
点评:此题属于解三角形的题型,涉及的知识有:正弦定理,正弦函数的图象与性质,正弦函数的定义域和值域,以及特殊角的三角函数值,考查了学生综合分析问题及基本运算的能力,熟练掌握定理及性质是解本题的关键.

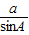 =
=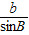 =2
=2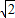 ,
,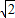 sinA,
sinA,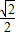 ,或sinA=1,
,或sinA=1,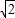 sinA,
sinA,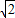 }.
}. }
}
