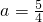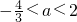Question

函数f（x）=x²-2（2a-1）x+8?（a∈R）．
（1）若f（x）在[2，+∞）的最小值为6，求a的值．
（2）若f（x）在[a，+∞）上为单调递增函数，且f（x）＞0，求实数a的取值范围．

Answer 1

解：由题意函数图象开口向上，且其对称轴为x=2a-1，
（1）当2a-1≥2，即a≥时，有f（x）_min=f（2a-1）=6
即（2a-1）²-2（2a-1）（2a-1）+8=6，即4a²-4a+9=6，即4a²-4a+3=0，由于△＜0，此方程无解
当2a-1＜2，即a＜时，有f（x）_min=f（2）=6
即4-4（2a-1）+8=6，解得a=＜，符合题意．
故
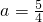
（2）若f（x）在[a，+∞）上为单调递增函数，由题意知，需要2a-1≤a，解得a≤1 ①
又由f（x）在[a，+∞）上为单调递增函数知f（a）＞0，即a²-2（2a-1）a+8＞0
解得
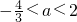
又由①得
故实数a的取值范围是
分析：函数f（x）=x²-2（2a-1）x+8图象开口向上，且其对称轴为x=2a-1，
（1）讨论对称轴与区间的位置，利用单调性确定出最小值在何处取到，利用最小最小值为6建立方程求参数a的值即可．
（2）本题要根据参数a的符号来确定函数在[a，+∞）上单调性与已知比对，来求参数a的范围．
点评：本题考点是二次函数的性质，考查利用二次函数的最值建立方程求参数，本题需要根据条件进行屋梁转化，且转化时要根据情况进行分类，题目有一定的综合性，做题时易考虑不完善造成失分．