
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 利用向量的模以及向量的数量积求解即可.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}}$=$\sqrt{5+4cos<\overrightarrow{a},\overrightarrow{b}>}$≤$\sqrt{9}$=3,当且仅当cos$<\overrightarrow{a},\overrightarrow{b}>$=1时,取等号.
故选:D.
点评 本题考查向量的数量积以及向量的模的求法,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{81\sqrt{3}}{8}$ | B. | $\frac{27\sqrt{3}}{4}$ | C. | 9$\sqrt{3}$ | D. | $\frac{27\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥γ,β⊥γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥β,那么平面α 中一定存在直线平行于平面β | |
| C. | 如果平面 α不垂直于平面β,那么平面α 内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥β,那么平面 α内所有直线都垂直于平面β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
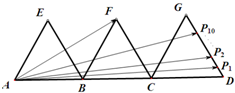 如图,三个边长为2的等边三角形有一条边在同一条直线上,边GD上有10个不同的点P1,P2,P3…P10,则$\overrightarrow{AF}$•($\overrightarrow{A{P_1}$+$\overrightarrow{A{P_2}}$+$\overrightarrow{A{P_3}}$+…+$\overrightarrow{A{P_{10}}}$)=180.
如图,三个边长为2的等边三角形有一条边在同一条直线上,边GD上有10个不同的点P1,P2,P3…P10,则$\overrightarrow{AF}$•($\overrightarrow{A{P_1}$+$\overrightarrow{A{P_2}}$+$\overrightarrow{A{P_3}}$+…+$\overrightarrow{A{P_{10}}}$)=180.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com