【题目】已知
，
分别是双曲线
的左顶点、右焦点，过的直线
与
的一条渐近线垂直且与另一条渐近线和
轴分别交于
，
两点.若
，则的离心率是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
由已知条件设出直线l的方程，与y＝﹣
x联立，求P点坐标，将x＝0带入直线l，求Q点坐标，由AP⊥AQ，知kAPkAQ，由此求离心率．
∵A，F分别是双曲线
的左顶点、右焦点，
∴A（﹣a，0）F（c，0），
∵过F的直线l与C的一条渐近线垂直，
且与另一条渐近线和y轴分别交于P，Q两点，
∴直线l的方程为：y＝﹣
，
直线l：y＝﹣与y＝﹣x联立：
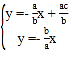，解得P点
将x＝0带入直线l：y＝﹣，得Q（0，
），
∵AP⊥AQ，∴kAPkAQ＝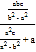
×
＝﹣1，
化简得b2﹣ac﹣a2＝﹣c2，
把b2＝c2﹣a2代入，得2c2﹣2a2﹣ac＝0
同除a2得2e2﹣2﹣e＝0，
∴e＝
，或e＝
（舍）．
故选：D．
科目：高中数学 来源： 题型：
【题目】设有一组圆
.下列四个命题正确的是（ ）
A. 存在
，使圆与
轴相切
B. 存在一条直线与所有的圆均相交
C. 存在一条直线与所有的圆均不相交
D. 所有的圆均不经过原点
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂生产甲、乙两种产品所得的利润分别为
和
（万元），事先根据相关资料得出它们与投入资金
（万元）的数据分别如下表和图所示：其中已知甲的利润模型为
，乙的利润模型为
．（
为参数，且
）.
|
|
|
|
|
|
|
|
|
|
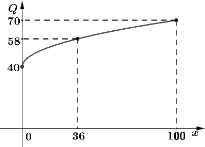
（1）请根据下表与图中数据，分别求出甲、乙两种产品所得的利润与投入资金（万元）的函数模型
（2）今将
万资金投入生产甲、乙两种产品，并要求对甲、乙两种产品的投入资金都不低于
万元．设对乙种产品投入资金
（万元），并设总利润为
（万元），如何分配投入资金，才能使总利润最大？并求出最大总利润．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(本题满分12分)
已知椭圆
的中心在原点，焦点在
轴上，椭圆上的点到焦点的距离的最
小值为
，离心率为
。
（I）求椭圆
的方程；
（Ⅱ）过点（1，0）作直线
交
于
、
两点，试问：在
轴上是否存在一个定点
，使
为定值？若存在，求出这个定点
的坐标；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的定义域为
，若存在区间
，使得
称区间为函数的“和谐区间”.
（1）请直接写出函数
的所有的“和谐区间”；
（2）若
为函数
的一个“和谐区间”，求
的值；
（3）求函数
的所有的“和谐区间”.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
且
）
（1）判断并证明
的奇偶性；
（2）求使
的
的取值范围；
（3）若
，是否存在实数
，使得
有三个不同的零点，若存在，求出的取值范围；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(1)讨论函数f(x)＝
ex的单调性，并证明当x>0时，(x－2)ex＋x＋2>0．
(2)证明：当a∈[0,1) 时，函数g(x)＝
(x>0) 有最小值．设g(x)的最小值为h(a)，求函数h(a)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
