
【题目】如图,等腰直角![]() 中
中![]() 是直角,平面
是直角,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
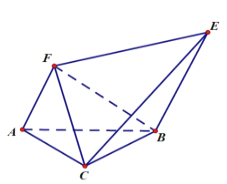
(1)求证![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由![]() 及
及![]() 为直角可得到
为直角可得到![]() ,结合已知条件命题得证。
,结合已知条件命题得证。
(2)作![]() ,连结
,连结![]() .由(1)得:
.由(1)得: ![]() ,作
,作![]() ,再证得:
,再证得:![]() 平面
平面![]() ,则
,则![]() 即为所求线面角. 解三角形BFH即可。
即为所求线面角. 解三角形BFH即可。
解:(1)证明:直角![]() 中∠B是直角,即
中∠B是直角,即![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() .
.
(2)方法一:作![]() ,连结
,连结![]() .
.
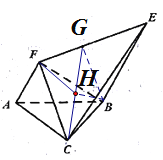
由(1)知![]() 平面
平面![]() ,
,
得到![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
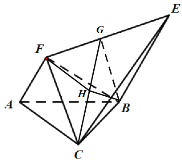
作![]() 于点H,易得
于点H,易得![]() 平面
平面![]() ,
,
则![]() 即为所求线面角.
即为所求线面角.
设![]() ,由已知得
,由已知得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
则直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
方法二:建立如图所示空间直角坐标系![]() ,
,
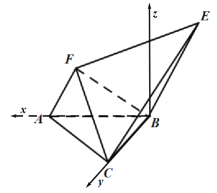
因为![]() .
.
由已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则有
,则有
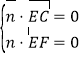 ,
,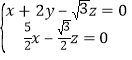 令
令![]() ,则
,则![]() .
.
即![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.
方法三(等积法):设2AF=AB=BE=2,![]() 为等腰三角形,AB=BC=2
为等腰三角形,AB=BC=2
∠FAB=60°,2AF=AB ![]() ,又AF//BE,
,又AF//BE,![]() .
.
由(1)知,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,则有
,则有![]() .
.
令![]() 到平面
到平面![]() 距离为
距离为![]() ,有
,有![]() ,
,
故所求线面角![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】随着中国经济的加速腾飞,现在手有余钱的中国家庭数量越来越多,在房价居高不下股市动荡不定的形势下,为了让自己的财富不缩水,很多家庭选择了投资理财.为了了解居民购买理财产品的情况,理财公司抽样调查了该市2018年10户家庭的年收入和年购买理财产品支出的情况,统计资料如下表:
年收入x(万元) | 20 | 40 | 40 | 60 | 60 | 60 | 70 | 70 | 80 | 100 |
年理财产品支出y(万元) | 9 | 14 | 16 | 20 | 21 | 19 | 18 | 21 | 22 | 23 |
(1)由该样本的散点图可知y与x具有线性相关关系,请求出回归方程;(求![]() 时利用
时利用![]() 的准确值,
的准确值,![]() ,
,![]() 的最终结果精确到0.01)
的最终结果精确到0.01)
(2)若某家庭年收入为120万元,预测某年购买理财产品的支出.(参考数据:![]() ,
,![]() ,
, ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数f(x),若存在区间[m,n]![]() D,同时满足下列条件:①f(x)在[m,n]上是单调的;②当定义域是[m,n]时,f(x)的值域也是[m,n],则称[m,n]为该函数的“和谐区间”.下列函数存在“和谐区间”的有( )
D,同时满足下列条件:①f(x)在[m,n]上是单调的;②当定义域是[m,n]时,f(x)的值域也是[m,n],则称[m,n]为该函数的“和谐区间”.下列函数存在“和谐区间”的有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,新型冠状病毒感染的肺炎疫情防控形势严峻.口罩的市场需求一直居高不下.为了保障防疫物资供应,潍坊的口罩企业加足马力保生产,上演了一场与时间赛跑的“防疫阻击战”.潍坊市坊子区一家口罩生产企业拥有1000平方米洁净车间,配备国际领先的自动化生产线5条,技术骨干20余人.自疫情发生以来,该企业积极响应政府号召,保障每天生产一次性无纺布健康防护口罩5万只左右.现从生产的大量口罩中抽取了100只作为样本,检测一项质量指标值,该项质量指标值落在区间[20,40)内的产品视为合格品,否则视为不合格品,如图是样本的频率分布直方图.

(1)求图中实数a的值;
(2)企业将不合格品全部销毁后,对合格品进行等级细分:质量指标值落在区间[25,30)内的定为一等品,每件售价2.4元;质量指标值落在区间[20,25)或[30,35)内的定为二等品,每件售价为1.8元;其他的合格品定为三等品,每件售价为1.2元.
用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.若有一名顾客随机购买2只口罩支付的费用为X(单位:元).求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y万元有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
附注:①参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com