Question

2．给出下列命题：
（1）若0＜x＜$\frac{π}{2}$，则sinx＜x＜tanx．
（2）若-$\frac{π}{2}$＜x＜0，则sinx＜x＜tanx．
（3）设A，B，C是△ABC的三个内角，若A＞B＞C，则sinA＞sinB＞sinC．
（4）设A，B是钝角△ABC的两个锐角，则sinA＞cosB．
其中，正确命题的个数为（　　）

• A． 4
• B． 3
• C． 2
• D． 1

Answer 1

分析 （1）根据单位圆以及三角函数的性质进行判断．
（2）利用特殊值法进行排除，
（3）根据正弦定理进行判断
（4）利用特殊值法进行排除．

解答 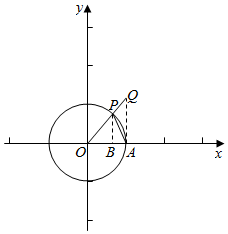解：（1）设角x的终边与单位圆的交点为P，PB⊥x轴，B为垂足，
单位圆和x轴的正半轴交于点A，AQ⊥x轴，且点Q∈OP，
如图所示，则|PB|=sinx，$\widehat{PA}$=x，|AQ|=tanx，
由于△POA的面积小于扇形POA的面积，扇形POA的面积小于
△AOQ的面积，
故有$\frac{1}{2}$|OA|•|PB|＜$\frac{1}{2}$$\widehat{PA}$•|OA|＜$\frac{1}{2}$|OA|•|AQ|，即|PB|＜$\widehat{PA}$＜|AQ|，即 sinx＜x＜tanx．故（1）正确，
（2）当x=-$\frac{π}{4}$时，sinx=-$\frac{\sqrt{2}}{2}$，tanx=-1，则sinx＞tanx，则sinx＜x＜tanx不成立，故（2）错误，
（3）设A，B，C是△ABC的三个内角，若A＞B＞C，则a＞b＞c，由正弦定理得sinA＞sinB＞sinC．故（3）正确，
（4）设A，B是钝角△ABC的两个锐角，当C=120°，A=B=30°时，满足条件．但sinA=$\frac{1}{2}$，cosB=$\frac{\sqrt{3}}{2}$．
则sinA＞cosB不成立，故（4）错误，
故正确的是（1）（3），
故选：C

点评 本题主要考查命题的真假判断，涉及三角函数的图象和性质以及解三角形的应用，涉及的知识点较多，但难度不大．