
分析 根据二项式(2x4-$\frac{1}{{x}^{3}}$)n展开式的通项公式,令展开式含x项的指数为3,求出r与n的关系,再求满足条件的最小正整数即可.
解答 解:二项式(2x4-$\frac{1}{{x}^{3}}$)n(n∈N+)展开式的通项公式为:
Tr+1=Cnr•(2x4)n-r•${(-\frac{1}{{x}^{3}})}^{r}$=(-1)r•2n-r•Cnr•x4n-7r;
令4n-7r=3,
即7r=4n-3,
解得r=$\frac{4n-3}{7}$,
所以4n-3是7的倍数;
所以满足条件的最小正整数是6.
故答案为:6.
点评 本题主要考查二项式定理的应用问题.解题的关键是利用展开式中x的指数等于3,求出r和n的关系.是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
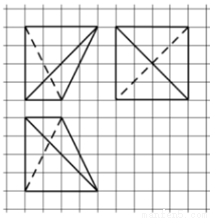
如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的外接球半径为( )
A.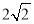 B.
B.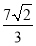 C.
C.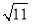 D.
D.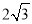
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com