
分析 讨论当直线BC与x轴垂直时,对任一个m,均有ABC为等边三角形;设直线BC的方程为y=kx+t(k≠0),代入双曲线的方程,运用韦达定理和中点坐标公式、以及两直线垂直的条件:斜率之积为-1,结合等边三角形的高与边长的关系,由不等式的性质,计算即可得到所求范围.
解答 解:当直线BC与x轴垂直时,对任一个m,均有ABC为等边三角形;
设直线BC的方程为y=kx+t(k≠0),代入双曲线的方程,可得
(1-k2)x2-2ktx-t2-1=0,
设B(x1,y1),C(x2,y2),可得
判别式为4k2t2+4(1-k2)(t2+1)>0,即t2+1-k2>0,
x1+x2=$\frac{2kt}{1-{k}^{2}}$>0,x1x2=-$\frac{1+{t}^{2}}{1-{k}^{2}}$>0,可得k2>1.
均有BC的中点M为($\frac{kt}{1-{k}^{2}}$,$\frac{t}{1-{k}^{2}}$),
|BC|=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{4{k}^{2}{t}^{2}}{(1-{k}^{2})^{2}}+\frac{4(1+{t}^{2})}{1-{k}^{2}}}$,
由AM⊥BC,可得kAM=-$\frac{1}{k}$,
均有$\frac{t}{kt-m+m{k}^{2}}$=-$\frac{1}{k}$,均有2kt=m(1-k2),
即t=$\frac{m(1-{k}^{2})}{2k}$,①
由A到直线BC的距离为d=$\frac{|km+t|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{3}}{2}$•$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{4{k}^{2}{t}^{2}}{(1-{k}^{2})^{2}}+\frac{4(1+{t}^{2})}{1-{k}^{2}}}$,
两边平方,将①代入,化简可得,m2=$\frac{6{k}^{2}}{{k}^{2}-1}$=6+$\frac{6}{{k}^{2}-1}$>6,
即有m>$\sqrt{6}$或m<-$\sqrt{6}$.
由双曲线的对称性可得,范围内有一个m,即有两个k的值,以及k不存在的情况.
故答案为:($\sqrt{6}$,+∞)∪(-∞,-$\sqrt{6}$).
点评 本题考查双曲线的方程和性质,注意运用对称性,讨论直线的斜率不存在和存在,联立直线方程和双曲线的方程,运用韦达定理和中点坐标公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
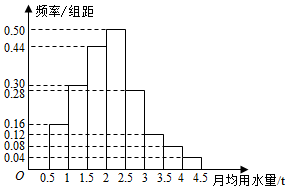
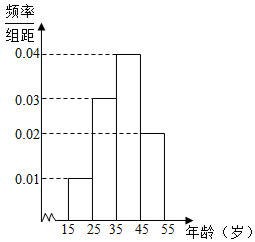 某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.
某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
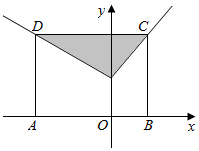 如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com