Question

【题目】已知函数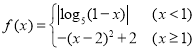,则关于的方程的实根个数构成的集合为_________.

Answer 1

【答案】

【解析】

画出的图像.令，并画出图像，结合两个函数图像以及，判断出实根个数构成的集合.

画出的图像如图所示.令，画出图像如图所示.

由解得.由，解得.

由解得.由，解得..

由解得.由，解得.

（1）当时，，有解，且或，结合的图像可知，每个都有两个与其对应，故此时有个实数根.

（2）当时，，有解，且或或，结合的图像可知，每个都有两个与其对应，故此时有个实数根.

（3）当时，，有解，且或或或，结合的图像可知，每个都有两个与其对应，故此时有个实数根.

（4）当时，，有解，且或或或，结合的图像可知，其中对应一个，其它三个都有两个与其对应，故此时有个实数根.

（5）当时，，有解，且或或，结合的图像可知，时没有与其对应，或时每个都有个与其对应，故此时有个实数根.

（6）当时，，有解，且或，有一个与其对应，有两个与其对应，故此时有个实数根.

（7）当时，，有解，且，结合的图像可知，每个有两个与其对应，故此时有个实数根.

综上所述，关于的方程的实根个数构成的集合为.

故答案为：