
分析 去绝对值号即可得到$f(x)=\left\{\begin{array}{l}{{x}^{2}-4x+3}&{x≥0}\\{{x}^{2}+4x+3}&{x<0}\end{array}\right.$,根据二次函数的单调性便可分别求出x≥0和x<0时的f(x)的单调区间,最后便可得出f(x)的单调区间.
解答 解:$f(x)={x}^{2}-4|x|+3=\left\{\begin{array}{l}{{x}^{2}-4x+3}&{x≥0}\\{{x}^{2}+4x+3}&{x<0}\end{array}\right.$;
∴①x≥0时,f(x)=x2-4x+3的对称轴为x=2;
∴f(x)在[0,2]上单调递减,在(2,+∞)上单调递增;
②x<0时,f(x)=x2+4x+3的对称轴为x=-2;
∴f(x)在(-∞,-2)上单调递减,在[-2,0)上单调递增;
∴f(x)的单调减区间为(-∞,-2),[0,2],单调增区间为[-2,0),(2,+∞).
点评 考查函数单调区间的定义及求法,含绝对值函数的处理方法:去绝对值号,分段函数单调性的判断,以及二次函数单调区间的求法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | π | C. | $\frac{2π}{3}-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
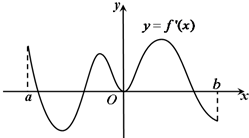 函数f(x)的导函数f′(x)在区间(a,b)内的图象如图所示,则f(x)在(a,b)内的极大值点有( )
函数f(x)的导函数f′(x)在区间(a,b)内的图象如图所示,则f(x)在(a,b)内的极大值点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
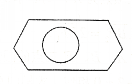 如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置可能性相等),恰有27粒落入半径为1的圆内,则该多边形的面积约为( )
如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置可能性相等),恰有27粒落入半径为1的圆内,则该多边形的面积约为( )| A. | 4π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 棱台的侧面一定不会是平行四边形 | |
| B. | 棱锥的侧面只能是三角形 | |
| C. | 由四个面围成的封闭图形只能是三棱锥 | |
| D. | 棱锥被平面截成的两部分不可能都是棱锥 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {4} | C. | {2,4} | D. | {2,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com