已知sint+cost=1,设s=cost+isint,求f(s)=1+s+s2+…sn.
【答案】
分析:本题考查的知识点是复数的运算,所要用到的数学思想是分类讨论思想,由sint+cost=1,我们易得:cost=0,sint=1或cost=1,sint=0,然后分类讨论两种情况,最后对各种进行总结,即可得到答案.
解答:解:sint+cost=1
∴(sint+cost)
2=1+2sint•cost=1
∴2sint•cost=sin2t=0
则cost=0,sint=1或cost=1,sint=0,
当cost=0,sint=1时,s=cost+isint=i
则f(s)=1+s+s
2+…s
n=
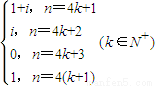
当cost=1,sint=0时,s=cost+isint=1
则f(s)=1+s+s
2+…s
n=n+1
点评:本题中第一情况主要考查了复数单位i的运算,要注意:
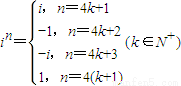

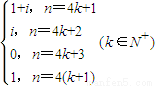
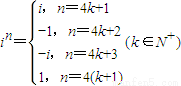


 阅读快车系列答案
阅读快车系列答案