
【题目】以双曲线![]() 上一点
上一点![]() 为圆心作圆,该圆与
为圆心作圆,该圆与![]() 轴相切于
轴相切于![]() 的一个焦点
的一个焦点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,若
两点,若![]() ,则双曲线
,则双曲线![]() 的离心率________.
的离心率________.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知集合![]() ,若对于任意实数对
,若对于任意实数对![]() ,存在
,存在![]() ,使
,使![]() 成立,则称集合
成立,则称集合![]() 是“垂直对点集” .给出下列四个集合:
是“垂直对点集” .给出下列四个集合:
① ![]() ;
;
②![]() ;
;
③ ![]() ;
;
④![]() .
.
其中是“垂直对点集”的序号是( ).
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数)上任意一点
为参数)上任意一点![]() 经过伸缩变换
经过伸缩变换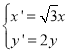 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数)上任意一点
为参数)上任意一点![]() 经过伸缩变换
经过伸缩变换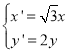 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学进行自主招生测试,需要对逻辑思维和阅读表达进行能力测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如图所示,下列叙述正确的是( )
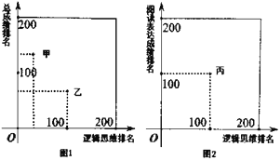
A.甲同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
B.乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
C.甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前
D.甲同学的总成绩排名比丙同学的总成绩排名更靠前
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司进行共享单车的投放与损耗统计,到去年![]() 年底单车的市场保有量(已投入市场且能正常使用的单车数量)为
年底单车的市场保有量(已投入市场且能正常使用的单车数量)为![]() 辆,预计今后每年新增单车1000辆,随着单车的频繁使用,估计每年将有200辆车的损耗,并且今后若干年内,年平均损耗在上一年损耗基础上增加
辆,预计今后每年新增单车1000辆,随着单车的频繁使用,估计每年将有200辆车的损耗,并且今后若干年内,年平均损耗在上一年损耗基础上增加![]() %.
%.
(1)预计![]() 年底单车的市场保有量是多少?
年底单车的市场保有量是多少?
(2)到哪一年底,市场的单车保有量达到最多?该年的单车保有量是多少辆(最后结果精确到整数)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com