
| x2 |
| 16 |
| y2 |
| 9 |
| 1 |
| 2 |
| 13 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
| 1 |
| 2 |
| 13 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
 解:由双曲线方程可得a=4,b=3,c=5,
解:由双曲线方程可得a=4,b=3,c=5,| 3x |
| 4 |
| 3x |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 9 |
|3×
| ||
|
| 13 |
| 8 |
| x2 |
| 16 |
| y2 |
| 9 |
|3×
| ||
|
| 7 |
| 8 |
| 1 |
| 2 |
| 13 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
| 1 |
| 2 |
| 13 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
| 4 |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知F1,F2分别是双曲线
已知F1,F2分别是双曲线| x2 |
| a2 |
| y2 |
| b2 |
| OH |
| ||
| 2 |
| F1M |
| MA |
查看答案和解析>>
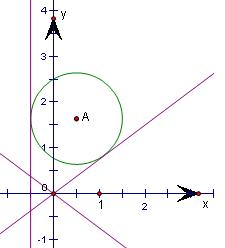
科目:高中数学 来源:2010-2011学年内蒙古高三第一次月考理科数学卷 题型:解答题
(本小题满分12分)
已知F1、F2分别是双曲线 的左、右焦点,以坐标原点O为圆心,以双曲线的半焦距c为半径的圆与双曲线在第一象限的交点为A,与y轴正半轴的交点为B,点A在y轴上的射影为H,且
的左、右焦点,以坐标原点O为圆心,以双曲线的半焦距c为半径的圆与双曲线在第一象限的交点为A,与y轴正半轴的交点为B,点A在y轴上的射影为H,且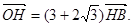
(I)求双曲线的离心率;
(II)若AF1交双曲线于点M,且 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
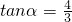 .将角α终边逆时针旋转
.将角α终边逆时针旋转 大小的角后与单位圆交于点Q,则点Q的坐标为
大小的角后与单位圆交于点Q,则点Q的坐标为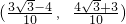
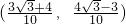
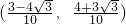
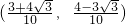
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 4 |
| 3 |
| π |
| 3 |
A.(
| B.(
| ||||||||||||||||
C.(
| D.(
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com