
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 有相同的焦点,且椭圆
有相同的焦点,且椭圆![]() 过点
过点![]() .
.
(I)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 与
与![]() 点不重合),且满足
点不重合),且满足![]() ,若点
,若点![]() 为
为![]() 中点,求直线
中点,求直线![]() 斜率的最大值.
斜率的最大值.

【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)写出抛物线焦点坐标,得椭圆中![]() ,把点
,把点![]() 的坐标代入椭圆方程得
的坐标代入椭圆方程得![]() 与
与![]() 联立可解得
联立可解得![]() ,得椭圆方程;
,得椭圆方程;
(Ⅱ)设![]() ,设直线方程为
,设直线方程为![]() ,与椭圆方程联立消元后应用教研室可得
,与椭圆方程联立消元后应用教研室可得![]() ,
,![]() ,用
,用![]() 代
代![]() 可得F点坐标,计算中点P坐标,计算AP的斜率为
可得F点坐标,计算中点P坐标,计算AP的斜率为![]() ,分子分母同时除以
,分子分母同时除以![]() ,并换元
,并换元![]() ,得
,得![]() ,由基本不等式可得最大值.
,由基本不等式可得最大值.
试题解析:
(Ⅰ)因为抛物线![]() 的焦点为
的焦点为![]() ,抛物线与椭圆C有相同的焦点
,抛物线与椭圆C有相同的焦点
所以![]() ,又椭圆
,又椭圆![]() 过点
过点![]() ,所以
,所以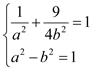 解得
解得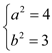 .
.
则椭圆的标准方程为![]() ;
;
(Ⅱ)设![]() ,
,![]()
直线AE的方程为![]() ,代入椭圆方程,可得
,代入椭圆方程,可得![]()
由![]() ,可得
,可得![]() ,
,![]() ,
,
由于AE⊥AF,只要将上式的![]() 换为
换为![]() ,可得
,可得![]() ,
,![]() ,
,
由P为EF的中点,得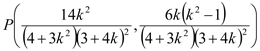
则直线AP的斜率为![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,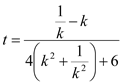 ,
,
再令![]() ,可得
,可得![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,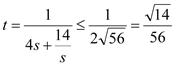 ,
,
当且仅当![]() 时,取得最大值;
时,取得最大值;
综上可得直线AP的斜率的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知A、B、C是△ABC的三个内角,则在下列各结论中,不正确的为( )
A. sin2A=sin2B+sin2C+2sinBsinCcos(B+C)
B. sin2B=sin2A+sin2C+2sinAsinCcos(A+C)
C. sin2C=sin2A+sin2B-2sinAsinBcosC
D. sin2(A+B)=sin2A+sin2B-2sinBsinCcos(A+B)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,若存在
,若存在![]() ,满足
,满足![]() ,则称
,则称![]() 是
是![]() 的一个“友好”三角形.
的一个“友好”三角形.
(ⅰ)在满足下述条件的三角形中,存在“友好”三角形的是__________;(请写出符合要求的条件的序号).
①![]() ,
,![]() ,
,![]() ; ②
; ②![]() ,
,![]() ,
,![]() ;
;
③![]() ,
,![]() ,
,![]() .
.
(ⅱ)若![]() 存在“友好”三角形,且
存在“友好”三角形,且![]() ,在另外两个角的度数分别为__________.
,在另外两个角的度数分别为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图:
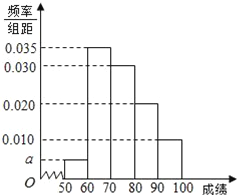
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)完游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)设![]() 分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况;
分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况;
(2)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜,你认为此游戏是否公平,说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() ,
, ![]() 均为非零向量,已知命题p:
均为非零向量,已知命题p: ![]() =
= ![]() 是
是 ![]()
![]() =
= ![]()
![]() 的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
A.p∧q
B.p∨q
C.(¬p)∧(¬q)
D.p∨(¬q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com