
【题目】用长为18cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
【答案】解:设长方体的宽为x(cm),则长为2x(cm),高为 ![]() .
.
故长方体的体积为V(x)=2x2(4.5﹣3x)=9x2﹣6x3(cm3) ![]() .
.
从而V′(x)=18x﹣18x2=18x(1﹣x).
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时,V′(x)>0;当1<x< ![]() 时,V′(x)<0,
时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值.
从而最大体积V=V′(x)=9×12﹣6×13(cm3),此时长方体的长为2cm,高为1.5cm.
答:当长方体的长为2cm时,宽为1cm,高为1.5cm时,体积最大,最大体积为3cm3 .
【解析】先设设长方体的宽为x(cm),利用长方体的体积公式求得其体积表达式,再利用导数研究它的单调性,进而得出此函数的最大值即可.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n个金属片从1号针移到3号针最少需要移动的次数记为f(n);
①f(3)=;
②f(n)= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数g(x)=mx2﹣2mx+n+1(m>0)在区间[0,3]上有最大值4,最小值0.
(1)求函数g(x)的解析式;
(2)设f(x)= ![]() .若f(2x)﹣k2x≤0在x∈[﹣3,3]时恒成立,求k的取值范围.
.若f(2x)﹣k2x≤0在x∈[﹣3,3]时恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,三角形ABC为等腰直角三角形,AC=BC= ![]() ,AA1=1,点D是AB的中点.
,AA1=1,点D是AB的中点. 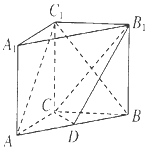
(1)求证:AC1∥平面CDB1;
(2)二面角B1﹣CD﹣B的平面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知长方形ABCD中,AB=2,AD=1,E为DC的中点.将△ADE沿AE折起,使得平面ADE⊥平面ABCE. 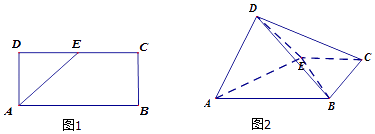
(1)求证:平面BDE⊥平面ADE
(2)求三棱锥 C﹣BDE的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由
是由![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() .现将
.现将![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]() 的大小为90°,得到图形如图(2)所示,连接
的大小为90°,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(Ⅰ)证明: ![]() ;
;
(Ⅱ)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且 PB=PC= ![]() .
.
(Ⅰ)求证:AB⊥CP;
(Ⅱ)求点B到平面PAD的距离;
(Ⅲ)设面PAD与面PBC的交线为l,求二面角A﹣l﹣B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com