
【题目】如图1,已知长方形ABCD中,AB=2,AD=1,E为DC的中点.将△ADE沿AE折起,使得平面ADE⊥平面ABCE. 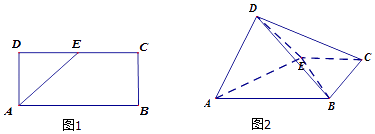
(1)求证:平面BDE⊥平面ADE
(2)求三棱锥 C﹣BDE的体积
【答案】
(1)证明:连接BE,∵长方形ABCD中,AB=2,AD=1,
E为DC的中点,DE=1,∴AE=BE= ![]()
∴AE2+BE2=2=AB2,∴BE⊥AE.
∵平面ADE⊥平面ABCE,平面ADE∩平面ABCE=AE,BE平面ABCE
∴BE⊥平面ADE,又∵BE平面BDE,
∴平面BDE⊥平面ADE
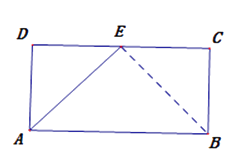
(2)解:取AE中点F,连结DF,
∵AD=DE,∴DF⊥AE,
又∵平面ADE⊥平面ABCE,且交线为AE,DF平面ADE,
∴DF⊥平面BCE
在Rt△ADE中,AD=DE=1,AE= ![]() ,∴DF=
,∴DF= ![]() ,
,
∴ ![]()
又∵VC﹣BED=VD﹣BCE,
∴三棱锥C﹣BDE的体积 ![]()

【解析】(1)连接BE,推民出BE⊥AE,从而BE⊥平面ADE,由此能证明平面BDE⊥平面ADE.(2)取AE中点F,连结DF,由VC﹣BED=VD﹣BCE , 能求出三棱锥C﹣BDE的体积.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】若函数fA(x)的定义域为A=[a,b),且fA(x)=( ![]() +
+ ![]() ﹣1)2﹣
﹣1)2﹣ ![]() +1,其中a,b为任意正实数,且a<b.
+1,其中a,b为任意正实数,且a<b.
(1)求函数fA(x)的最小值和最大值;
(2)若x1∈Ik=[k2 , (k+1)2),x2∈Ik+1=[(k+1)2 , (k+2)2),其中k是正整数,对一切正整数k,不等式 ![]() (x1)+
(x1)+ ![]() (x2))<m都有解,求m的取值范围;
(x2))<m都有解,求m的取值范围;
(3)若对任意x1 , x2 , x3∈A,都有 ![]() ,
, ![]() ,
, ![]() 为三边长构成三角形,求
为三边长构成三角形,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣x3+ax2+bx+c的导数f'(x)满足f'(﹣1)=0,f'(2)=9.
(1)求f(x)的单调区间;
(2)f(x)在区间[﹣2,2]上的最大值为20,求c的值.
(3)若函数f(x)的图象与x轴有三个交点,求c的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为18cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3﹣3ax2+3bx的图象与直线12x+y﹣1=0相切于点(1,﹣11).
(1)求a,b的值;
(2)讨论函数f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在矩形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面![]()
![]() 平面
平面![]() .
.
(1)在线段![]() 上确定点
上确定点![]() ,使得
,使得![]() 平面
平面![]() ,并证明;
,并证明;
(2)求![]() 与
与![]() 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,点A(﹣2,0),B(2,0),C(x,1) (i)若∠ACB是直角,则x=
(ii)若△ABC是锐角三角形,则x的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某班学生一次英语测验的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为( ) 
A.92%
B.24%
C.56%
D.5.6%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com