【题目】对某班学生一次英语测验的成绩分析，各分数段的分布如图（分数取整数），由此，估计这次测验的优秀率（不小于80分）为（ ） 
A.92%
B.24%
C.56%
D.5.6%
【答案】C
【解析】解：这次测验的优秀率（不小于80分）为
0.032×10+0.024×10=0.56
故这次测验的优秀率（不小于80分）为56%
故选C
【考点精析】通过灵活运用频率分布直方图和用样本的频率分布估计总体分布，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；样本数据的频率分布表和频率分布直方图，是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律，它可以让我们更清楚的看到整个样本数据的频率分布情况，并由此估计总体的分布情况即可以解答此题．
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】如图1，已知长方形ABCD中，AB=2，AD=1，E为DC的中点．将△ADE沿AE折起，使得平面ADE⊥平面ABCE．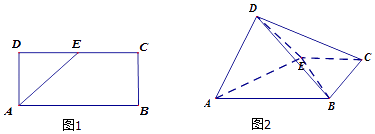 
（1）求证：平面BDE⊥平面ADE
（2）求三棱锥 C﹣BDE的体积
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图（1）所示，已知四边形
是由
和直角梯形
拼接而成的，其中
.且点
为线段
的中点， 
， 
.现将
沿
进行翻折，使得二面角
的大小为90°，得到图形如图（2）所示，连接
，点
分别在线段
上.
（Ⅰ）证明： 
；
（Ⅱ）若三棱锥
的体积为四棱锥
体积的
，求点
到平面
的距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax2+ln（x+1）．
（1）当a=﹣ 
时，求函数f（x）的单调区间；
（2）若函数f（x）在区间[1，+∞）上为减函数，求实数a的取值范围；
（3）当x∈[0，+∞）时，不等式f（x）﹣x≤0恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax3+bx2+cx在点x0处取得极大值5，其导函数y=f′（x）的图象经过点（1，0），（2，0），如图所示．求：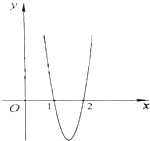
（1）x0的值；
（2）a，b，c的值．
（3）若曲线y=f（x）（0≤x≤2）与y=m有两个不同的交点，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，平面PBC⊥底面ABCD，且 PB=PC= 
．
（Ⅰ）求证：AB⊥CP；
（Ⅱ）求点B到平面PAD的距离；
（Ⅲ）设面PAD与面PBC的交线为l，求二面角A﹣l﹣B的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
