
【题目】为了完成对某城市的工薪阶层是否赞成调整个人所得税税率的调查,随机抽取了60人,作出了他们的月收入频率分布直方图(如图),同时得到了他们月收入情况与赞成人数统计表(如下表):
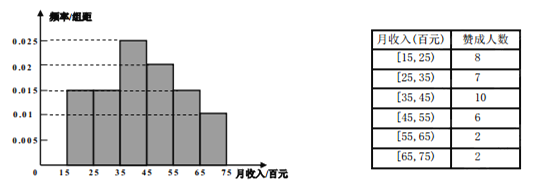
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求2人都不赞成的概率.
【答案】(1)这60人的平均月收入约为43.5百元.(2)![]()
【解析】试题分析:(1)由频率分布直方图中每组中横轴数据的中间值与纵轴数据乘积的和来估计所有数据的平均值;(2)由频率分布直方图和表格可知[65,75)共有![]() 人,其中
人,其中![]() 人赞成,
人赞成, ![]() 人不赞成,可写出任取
人不赞成,可写出任取![]() 人的所有情况,找出其中
人的所有情况,找出其中![]() 人都不赞成的情况,利用古典概型可得结果.
人都不赞成的情况,利用古典概型可得结果.
试题解析:(1)由直方图知:
![]()
![]() 这60人的平均月收入约为43.5百元.
这60人的平均月收入约为43.5百元.
(2)根据频率分布直方图和统计图表可知
[65,75)的人数为0.01×10×60=6人,其中2人赞成,4人不赞成
记赞成的人为x,y,不赞成的人为a,b,c,d
任取2人的情况分别是:xy,xa,xb,xc,xd,ya,yb,yc,yd,ab,ac,ad,bc,bd,cd共15种情况
其中2人都不赞成的是:ab,ac,ad,bc,bd,cd共6种情况
∴2人都不赞成的概率是:P=![]() .
.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,已知圆![]() 是
是![]() 的外接圆,
的外接圆, ![]() ,
,![]() 是
是![]() 边上的高,
边上的高,![]() 是圆
是圆![]() 的直径,过点
的直径,过点![]() 作圆
作圆![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
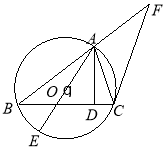
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
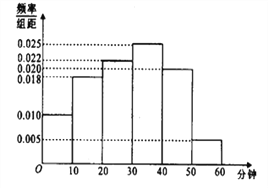
(Ⅰ)根据已知条件完成下面的![]() 列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(参考公式![]() ,其中
,其中![]() .)
.)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左焦点为
)的左焦点为![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 为坐标原点,
为坐标原点, ![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 作
作![]() 的垂线交椭圆于
的垂线交椭圆于![]() ,
, ![]() .当四边形
.当四边形![]() 是平行四边形时,求四边形
是平行四边形时,求四边形![]() 的面积。
的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象形如汉字“囧”,故称其为“囧函数”.
的图象形如汉字“囧”,故称其为“囧函数”.
下列命题:
①“囧函数”的值域为![]() ;
;
②“囧函数”在![]() 上单调递增;
上单调递增;
③“囧函数”的图象关于![]() 轴对称;
轴对称;
④“囧函数”有两个零点;
⑤“囧函数”的图象与直线![]()
至少有一个交点.正确命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到其两焦点
到其两焦点![]() ,
,![]() 的距离之和为
的距离之和为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且
,且![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
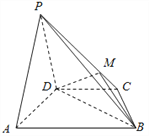
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com