
【题目】选修4—1:几何证明选讲
如图,已知圆![]() 是
是![]() 的外接圆,
的外接圆, ![]() ,
,![]() 是
是![]() 边上的高,
边上的高,![]() 是圆
是圆![]() 的直径,过点
的直径,过点![]() 作圆
作圆![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
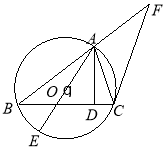
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】水是万物之本、生命之源,节约用水,从我做起.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
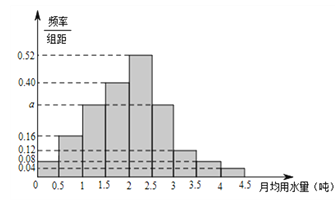
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)延长![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作抛物线的切线
作抛物线的切线![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
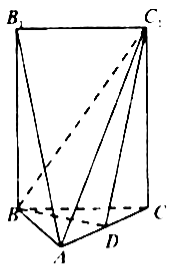
【题目】如图,五面体![]() 中,
中,![]() ,底面
,底面![]() 是正三角形,
是正三角形,![]() ,四边形
,四边形![]() 是矩形,二面角
是矩形,二面角![]() 为直二面角.
为直二面角.
(1)![]() 在
在![]() 上运动,当
上运动,当![]() 在何处时,有
在何处时,有![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)当![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 余弦值.
余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了完成对某城市的工薪阶层是否赞成调整个人所得税税率的调查,随机抽取了60人,作出了他们的月收入频率分布直方图(如图),同时得到了他们月收入情况与赞成人数统计表(如下表):
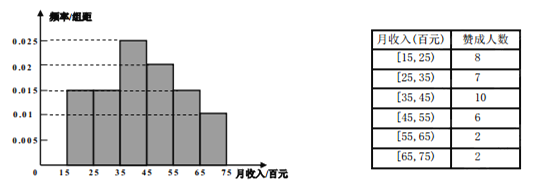
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求2人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
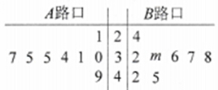
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com