
【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
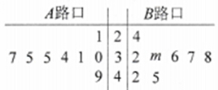
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由茎叶图可得![]() 路口
路口![]() 个数据中
个数据中![]() 为最中间两个数,由此计算中位数,又
为最中间两个数,由此计算中位数,又![]() 路口
路口![]() 个数据的平均数为
个数据的平均数为![]() ,可得
,可得![]() ;(2)
;(2)![]() 在路口的数据中任取
在路口的数据中任取![]() 个大于
个大于![]() 的数据,有
的数据,有![]() 种可能,其中“至少有一次抽取的数据不小于
种可能,其中“至少有一次抽取的数据不小于![]() ”的情况有
”的情况有![]() 种,故所求概率为
种,故所求概率为![]() .
.
试题解析:(1)![]() 路口8个数据的中位数为
路口8个数据的中位数为![]() .
.
∵![]() 路口8个数据的平均数为
路口8个数据的平均数为![]() ,
,
∴![]() 路口8个数据的平均数为36,
路口8个数据的平均数为36,
∴![]() ,
,![]() .
.
(2)![]() 在路口的数据中任取2个大于35的数据,有如下10种可能结果:
在路口的数据中任取2个大于35的数据,有如下10种可能结果:
(36,37),(36,38),(36,42),(36,45),(37,38),(37,42),(37,45),
(38,42),(38,45),(42,45).
其中“至少有一次抽取的数据不小于40”的情况有如下7种:
(36,42),(36,45),(37,42),(37,45),(38,42),(38,45),(42,45).
故所求的概率为![]()


科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,已知圆![]() 是
是![]() 的外接圆,
的外接圆, ![]() ,
,![]() 是
是![]() 边上的高,
边上的高,![]() 是圆
是圆![]() 的直径,过点
的直径,过点![]() 作圆
作圆![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
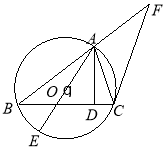
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到其两焦点
到其两焦点![]() ,
,![]() 的距离之和为
的距离之和为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且
,且![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
“健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如下:

(I)求李老师这8天“健步走”步数的平均数;
(II)从步数为16千步,17千步,18千步的6天中任选2天,设李老师这2天通过“健步走”消耗的能量和为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,短轴长为2,
,短轴长为2,![]() 为原点,直线
为原点,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,且
,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
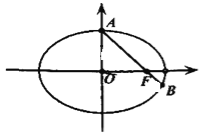
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若在椭圆
两点,若在椭圆![]() 上存在点
上存在点![]() ,使
,使![]() 为平行四边形,求
为平行四边形,求![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
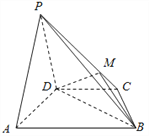
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(1)求曲线![]() 与
与![]() 的交点
的交点![]() 的直角坐标;
的直角坐标;
(2)设点![]() ,
, ![]() 分别为曲线
分别为曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com