
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
| p(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$,求出喜欢吃辣的有$\frac{3}{5}×100=60$,可得2×2列联表;
(2)求出k2,与是临界值比较,即可得出是否有99.9%以上的把握认为喜欢吃辣与性别有关
解答 解:(1)∵在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$.
∴在100人中,喜欢吃辣的有$\frac{3}{5}×100=60$…(2分)
∴男生喜欢吃辣的有60-20=40,
列表补充如下:
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
点评 本题考查独立性检验的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F1在以$Q(-\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F1在以$Q(-\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)≤f(2)≤f(4) | B. | f(2)>f(1)>f(4) | C. | f(2)<f(4)<f(1) | D. | f(4)>f(2)>f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
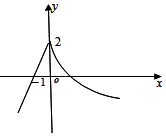
| A. | $\frac{10}{3}$ | B. | $\frac{13}{3}$ | C. | 3 | D. | $\frac{9}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com