
分析 由已知得an=Sn-Sn-1=-3n+104,该等差数列为101,98,89,…前34项为正,由此能求出数列{|an|}的前n项的和Tn.
解答 解:∵等差数列{an}的前n项和Sn=-$\frac{3}{2}$n2+$\frac{205}{2}$n,
∴an=Sn-Sn-1=(-$\frac{3}{2}$n2+$\frac{205}{2}$n)-[-$\frac{3}{2}$(n-1)2+$\frac{205}{2}$(n-1))]=-3n+104,
该等差数列为101,98,89,…前34项为正,其前34项和公式为Tn=-$\frac{3}{2}$n2+$\frac{205}{2}$n,
∴n≥35时,Tn=$\frac{3}{2}$n2-$\frac{205}{2}$n+3520,
∴Tn=$\left\{\begin{array}{l}{-\frac{3}{2}{n}^{2}+\frac{205}{2}n(n≤34)}\\{\frac{3}{2}{n}^{2}-\frac{205}{2}n+3502(n≥35)}\end{array}\right.$.
故答案是:$\left\{\begin{array}{l}{-\frac{3}{2}{n}^{2}+\frac{205}{2}n(n≤34)}\\{\frac{3}{2}{n}^{2}-\frac{205}{2}n+3502(n≥35)}\end{array}\right.$.
点评 本题考查等差数列的前n项的绝对值的和的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
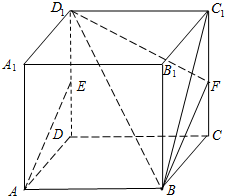 在正方体ABCD-A1B1C1D1中,E、F分别为DD1、CC1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别为DD1、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n<m | B. | n>m | C. | n=m | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com