
分析 (1)利用任意角的三角函数的定义,求得sinα的值,可得$f(\frac{α}{2}-\frac{π}{12})$的值;
(2)根据$x∈[-\frac{π}{6},\frac{π}{3}]$,利用正弦函数的定义域和值域,求得f(x)的值域.
解答 解:(1)∵点$P(1,-\sqrt{3})$在角α的终边上,∴$sinα=\frac{{-\sqrt{3}}}{{\sqrt{{1^2}+{{(-\sqrt{3})}^2}}}}=-\frac{{\sqrt{3}}}{2}$,
∴$f(\frac{α}{2}-\frac{π}{12})=2sin[2(\frac{α}{2}-\frac{π}{12})+\frac{π}{6}]=2sinα=-\sqrt{3}$.
(2)∵$x∈[-\frac{π}{6},\frac{π}{3}]$,∴$2x+\frac{π}{6}∈[-\frac{π}{6},\frac{5π}{6}]$,∴$-\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$,
∴$-1≤2sin(2x+\frac{π}{6})≤2$,即函数的值域为[-1,2].
点评 本题主要考查任意角的三角函数的定义,正弦函数的定义域和值域,属于中档题.


科目:高中数学 来源: 题型:解答题
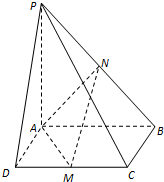 如图:已知四棱锥P-ABCD,底面是边长为6的正方形,PA=8,PA⊥面ABCD,
如图:已知四棱锥P-ABCD,底面是边长为6的正方形,PA=8,PA⊥面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com