
分析 (1)根据绝对值的几何意义即可得到答案.
(2)由条件可得:$\frac{1}{4|b|}$+$\frac{|b|}{a}$的“1”用a+b替换,b>0,b<0,去掉绝对值,利用基本不等式求其最小值.比较即可得到答案
(3)等式两边取倒,得:$\frac{1}{y}=\frac{{a}^{2}+1}{2a}$,分离可得$\frac{a}{2}+\frac{1}{2a}=\frac{1}{y}$,利用基本不等式求其最小值,当且仅当a=1时取等号.而a≥2,则考虑其单调性即可得到范围.
解答 解:(1)根据绝对值的几何意义:
|x-1|+|x-3的最小值是2,|
要使|x-1|+|x-3|≥a2+a恒成立,只需2≥a2+a,
解得:-2≤a≤1
(2)∵a+b=1,
∴$\frac{1}{4|b|}$+$\frac{|b|}{a}$=$\frac{a+b}{4|b|}+\frac{|b|}{a}$=$\frac{a}{4|b|}+\frac{b}{4|b|}+\frac{|b|}{a}$
当b>0时:$\frac{a}{4|b|}+\frac{b}{4|b|}+\frac{|b|}{a}$=$\frac{1}{4}+\frac{a}{4b}+\frac{b}{a}$$≥2\sqrt{\frac{a}{4b}•\frac{b}{a}}+\frac{1}{4}=\frac{5}{4}$当且仅当a=$\frac{2}{3}$,b=$\frac{1}{3}$时取等号)
当b<0时:$\frac{a}{4|b|}+\frac{b}{4|b|}+\frac{|b|}{a}$=$\frac{a}{4b}+\frac{b}{a}-\frac{1}{4}$$≥2\sqrt{\frac{a}{4b}•\frac{b}{a}}-\frac{1}{4}=\frac{3}{4}$(当且仅当a=2,b=-1时取等号)
由上述可知:$\frac{1}{4|b|}$+$\frac{|b|}{a}$的最小值为$\frac{3}{4}$,取得最小值时a的值等于2;
(3)y=$\frac{2a}{{{a^2}+1}}$,
等式两边取倒,得:$\frac{1}{y}=\frac{{a}^{2}+1}{2a}$,分离可得$\frac{a}{2}+\frac{1}{2a}=\frac{1}{y}$,
∵$\frac{a}{2}+\frac{1}{2a}≥2\sqrt{\frac{a}{2}•\frac{1}{2a}}=1$,当且仅当a=1时取等号.此时y的最大值为1.
而a≥2,则考虑其单调性
设:2≤a1<a2
那么:f(a2)-f(a1)=$\frac{2{a}_{2}}{{1+{a}_{2}}^{2}}-\frac{2{a}_{1}}{1+{{a}_{1}}^{2}}$=$\frac{2{a}_{2}+2{a}_{2}{{a}_{1}}^{2}-2{a}_{1}-2{a}_{1}{{a}_{2}}^{2}}{(1+{{a}_{1}}^{2})(1+{{a}_{2}}^{2})}$
分母恒大于0,
化简分子,得:2(a2-a1)-2a1a2(a2-a1)=(2-2a1a2)(a2-1a)<0
∴f(a2)-f(a1)<0 所以:a∈[2,+∞)y是单调减函数.
当a∈[2,+∞)时,y是单调减函数,
∴a=2时,y取得最大值,即:y=$\frac{2×2}{{1+2}^{2}}=\frac{4}{5}$
又∵a>0,∴y=$\frac{2a}{{{a^2}+1}}$>0
所以:y=$\frac{2a}{{{a^2}+1}}$,a∈[2,+∞)的取值范围是(0,$\frac{4}{5}$]
点评 本题考查了基本不等式的性质、绝对值不等式的解法,考查了计算能力,注意:当利用基本不等式求其最小值(或最大值)时,当且仅当取等号的值不在其范围内时.则考虑其单调性.属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 个人家庭用车消费汽油费 | ≤880元/月 | 880~920元/月 | 920~940元/月 | ≥940元/月 |
| 税 率 | 不纳税 | 0.01 | 0.02 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
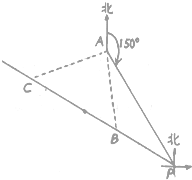 海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.
海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com